
【题目】已知正三棱锥P﹣ABC中E,F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P﹣ABC的外接球的表面积( )
A.4π
B.6π
C.8π
D.12π
科目:高中数学 来源: 题型:
【题目】“微信运动”是腾讯开发的一个记录跑步或行走情况(步数里程)的公众号用户通过该公众号可查看自己某时间段的运动情况.某人根据2018年1月至2018年11月期间每月离步的里程(单位:十公里)的数据绘制了下面的折线图.根据该折线图,下列结论正确的是( )

A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂新研发了一种产品,该产品每件成本为5元,将该产品按事先拟定的价格进行销售,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求销量![]() (件)关于单价
(件)关于单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(2)若单价定为10元,估计销量为多少件;
(3)根据销量![]() 关于单价
关于单价![]() 的线性回归方程,要使利润
的线性回归方程,要使利润![]() 最大,应将价格定为多少?
最大,应将价格定为多少?
参考公式: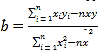 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某市供电公司数据,2019年1月份市新能源汽车充电量约270万度,同比2018年增长![]() ,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照
,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照![]() ,
,![]() ,…,
,…,![]() 分成5组,制成如图所示的频率分布直方图.
分成5组,制成如图所示的频率分布直方图.
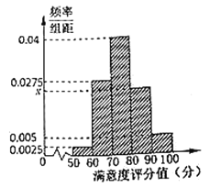
(1)求图中![]() 的值并估计样本数据的中位数;
的值并估计样本数据的中位数;
(2)已知满意度评分值在![]() 内的男女司机人数比为
内的男女司机人数比为![]() ,从中随机抽取2人进行座谈,求2人均为女司机的概率.
,从中随机抽取2人进行座谈,求2人均为女司机的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.则函数y=f(x)( )
A.有极小值,无极大值
B.有极大值,无极小值
C.既有极小值又有极大值
D.既无极小值又无极大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com