
【题目】知函数![]() ,
,![]() ,
,![]() 与
与![]() 在交点
在交点![]() 处的切线相互垂直.
处的切线相互垂直.
(1)求![]() 的解析式;
的解析式;
(2)已知![]() ,若函数
,若函数![]() 有两个零点,求
有两个零点,求![]() 的取值范围 .
的取值范围 .
【答案】(1) ![]() 。
。
(2) ![]() 或
或![]() 。
。
【解析】分析:(1)分别求出![]() 与
与![]() 在交点
在交点![]() 处切线的斜率,从而得到答案;
处切线的斜率,从而得到答案;
(2)对![]() 求导,分类讨论即可.
求导,分类讨论即可.
详解:(1) ![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 与
与![]() 在交点
在交点![]() 处的切线相互垂直,
处的切线相互垂直,
![]() ,
,![]() .又
.又![]() 在
在![]() 上,
上, ![]() ,
,
故![]() .
.
(2)由题知![]()
![]()
![]()
![]()
![]() .
.
①![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() 或
或![]() ,
,
![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,故存在
上单调递增,故存在![]() 使
使
![]()
![]()
![]() .又
.又![]() ,
,![]() ,
,![]() ,
,
![]() 在区间
在区间![]() 上有一个零点,在区间
上有一个零点,在区间![]() 上有一个零点,
上有一个零点,
在区间![]() 上有一个零点,共
上有一个零点,共![]() 个零点,不符合题意,舍去.
个零点,不符合题意,舍去.
②![]() 时,令
时,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,
,
![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,![]() 有两个零点,符合题意.
有两个零点,符合题意.
③![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() 或
或![]() ,
,
![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
![]() ,
,![]() 在区间
在区间![]() 上存在一个零点,
上存在一个零点,
若要![]() 有两个零点,必有
有两个零点,必有![]() ,解得
,解得![]() .
.
④![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,
,
![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
![]() ,
,![]() 在区间
在区间![]() 上存在一个零点,
上存在一个零点,
又![]()
![]()
![]()
![]()
![]() ,
,
∴在区间∴上不存在零点,即![]() 只有一个零点,不符合题意.
只有一个零点,不符合题意.
综上所述, ![]() 或
或![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,各个侧面均是边长为
中,各个侧面均是边长为![]() 的正方形,
的正方形,![]() 为线段
为线段![]() 的中点.
的中点.
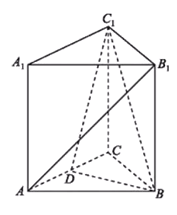
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)设![]() 为线段
为线段![]() 上任意一点,在
上任意一点,在![]() 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=3cos2x的图象,只需把函数y=3sin(2x+ ![]() )的图象上所有的点( )
)的图象上所有的点( )
A.向右平行移动 ![]() 个单位长度
个单位长度
B.向右平行移动 ![]() 个单位长度
个单位长度
C.向左平行移动 ![]() 个单位长度
个单位长度
D.向左平移移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
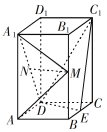
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),且原点、焦点,短轴的端点构成等腰直角三角形.
),且原点、焦点,短轴的端点构成等腰直角三角形.
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() ?若存在,求出该圆的方程,若不存在说明理由.
?若存在,求出该圆的方程,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年04月13日“山东济南非法经营疫苗系列案件”披露后,引发社会高度关注,引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧。为采取后续处置措施提供依据,保障受种者的健康,尽快恢复公众接种疫苗的信心,科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效,对某疫苗预防疾病的效果,进行动物实验,得到下面表格中的统计数据:现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
未发病 | 发病 | 合计 | |
未注射疫苗 |
|
|
|
注射疫苗 |
|
|
|
合计 |
|
|
|
(1)求![]() 列联表中的数据
列联表中的数据![]() 的值;
的值;
(2)绘制发病率的条形统计图,并判断疫苗是否有效?

|
|
|
|
|
|
|
|
|
|
(3)能够有多大把握认为疫苗有效?
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=2,D,E,F分别是B1A1 , CC1 , BC的中点,AE⊥A1B1 , D为棱A1B1上的点. 
(1)证明:DF⊥AE;
(2)求平面DEF与平面ABC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三棱锥P﹣ABC中E,F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P﹣ABC的外接球的表面积( )
A.4π
B.6π
C.8π
D.12π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com