
【题目】设椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),且原点、焦点,短轴的端点构成等腰直角三角形.
),且原点、焦点,短轴的端点构成等腰直角三角形.
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() ?若存在,求出该圆的方程,若不存在说明理由.
?若存在,求出该圆的方程,若不存在说明理由.
【答案】
(1)解:∵原点、焦点,短轴的端点构成等腰直角三角形,∴b=c,
∵椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),∴
),∴ ![]() =1,
=1,
联立 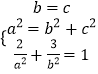 ,解得b=c=2,a2=8.
,解得b=c=2,a2=8.
∴椭圆E的方程为 ![]() =1
=1
(2)解:假设存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() .
.
设圆的方程为:x2+y2=r2,(0<r<2).
设圆的切线为y=kx+m,则 ![]() =r,A(x1,y1),B(x2,y2).
=r,A(x1,y1),B(x2,y2).
联立 ![]() ,化为:(1+2k2)x2+4kmx+2m2﹣8=0,
,化为:(1+2k2)x2+4kmx+2m2﹣8=0,
△≥0,可得:9k2+4≥m2.
x1+x2= ![]() ,x1x2=
,x1x2= ![]() .
.
∵ ![]() ,∴
,∴ ![]() =x1x2+y1y2=0.
=x1x2+y1y2=0.
∴(1+k2)x1x2+mk(x1+x2)+m2=0,
∴ ![]() ﹣
﹣ ![]() +m2=0,
+m2=0,
化为:3m2=8+8k2,与 ![]() =r联立,
=r联立,
可得r2= ![]() =
= ![]() =
= ![]() <4,
<4,
因此假设成立,存在圆心在原点的圆,方程为x2+y2= ![]() ,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B,且
,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B,且 ![]()
【解析】(1)由原点、焦点,短轴的端点构成等腰直角三角形,可得b=c.由椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),可得
),可得 ![]() =1,与a2=b2+c2联立即可得出.(2)假设存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且
=1,与a2=b2+c2联立即可得出.(2)假设存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() .设圆的方程为:x2+y2=r2 , (0<r<2).设圆的切线为y=kx+m,可得
.设圆的方程为:x2+y2=r2 , (0<r<2).设圆的切线为y=kx+m,可得 ![]() =r,A(x1 , y1),B(x2 , y2).与椭圆方程联立化为:(1+2k2)x2+4kmx+2m2﹣8=0,利用根与系数的关系及其
=r,A(x1 , y1),B(x2 , y2).与椭圆方程联立化为:(1+2k2)x2+4kmx+2m2﹣8=0,利用根与系数的关系及其 ![]() ,可得
,可得 ![]() =x1x2+y1y2=0.化简整理即可得出.
=x1x2+y1y2=0.化简整理即可得出.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 (t为参数)曲线C的参数方程为
(t为参数)曲线C的参数方程为![]() ,
,![]() 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为![]()
(![]() Ⅰ)求直线l以及曲线C的极坐标方程;
Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A、B两点,求三角形PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扇形AOB中心角为![]() ,所在圆半径为
,所在圆半径为![]() ,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.
,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.

(1)矩形CDEF的顶点C、D在扇形的半径OB上,顶点E在圆弧AB上,顶点F在半径OA上,设![]() ;
;
(2)点M是圆弧AB的中点,矩形CDEF的顶点D、E在圆弧AB上,且关于直线OM对称,顶点C、F分别在半径OB、OA上,设![]() ;
;
试研究(1)(2)两种方式下矩形面积的最大值,并说明两种方式下哪一种矩形面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这200名学生的平均分;
(3)若这200名学生的数学成绩中,某些分数段的人数![]() 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数![]() 之比如下表所示,求英语成绩在
之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 |
|
|
|
|
|
| 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某实验单次成功的概率为0.8,记事件A为“在实验条件相同的情况下,重复3次实验,各次实验互不影响,则3次实验中至少成功2次”,现采用随机模拟的方法估计事件4的概率:先由计算机给出0~9十个整数值的随机数,指定0,1表示单次实验失败,2,3,4,5,6,7,8,9表示单次实验成功,以3个随机数为组,代表3次实验的结果经随机模拟产生了20组随机数,如下表:
752 | 029 | 714 | 985 | 034 |
437 | 863 | 694 | 141 | 469 |
037 | 623 | 804 | 601 | 366 |
959 | 742 | 761 | 428 | 261 |
根据以上方法及数据,估计事件A的概率为( )
A.0.384B.0.65C.0.9D.0.904
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com