
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
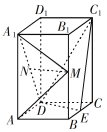
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)利用三角形中位线和![]() 可证得
可证得![]() ,证得四边形
,证得四边形![]() 为平行四边形,进而证得
为平行四边形,进而证得![]() ,根据线面平行判定定理可证得结论;(2)以菱形
,根据线面平行判定定理可证得结论;(2)以菱形![]() 对角线交点为原点可建立空间直角坐标系,通过取
对角线交点为原点可建立空间直角坐标系,通过取![]() 中点
中点![]() ,可证得
,可证得![]() 平面
平面![]() ,得到平面
,得到平面![]() 的法向量
的法向量![]() ;再通过向量法求得平面
;再通过向量法求得平面![]() 的法向量
的法向量![]() ,利用向量夹角公式求得两个法向量夹角的余弦值,进而可求得所求二面角的正弦值.
,利用向量夹角公式求得两个法向量夹角的余弦值,进而可求得所求二面角的正弦值.
(1)连接![]() ,
,![]()
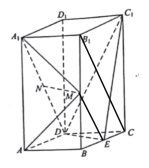
![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点
中点 ![]() 为
为![]() 的中位线
的中位线
![]() 且
且![]()
又![]() 为
为![]() 中点,且
中点,且![]()
![]() 且
且![]()
![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
(2)设![]() ,
,![]()
由直四棱柱性质可知:![]() 平面
平面![]()
![]() 四边形
四边形![]() 为菱形
为菱形 ![]()
则以![]() 为原点,可建立如下图所示的空间直角坐标系:
为原点,可建立如下图所示的空间直角坐标系:
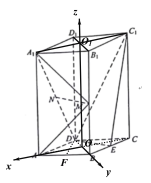
则:![]() ,
,![]() ,
,![]() ,D(0,-1,0)
,D(0,-1,0)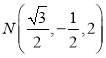
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则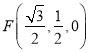
![]() 四边形
四边形![]() 为菱形且
为菱形且![]()
![]() 为等边三角形
为等边三角形 ![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() 平面
平面![]() ,即
,即![]() 平面
平面![]()
![]() 为平面
为平面![]() 的一个法向量,且
的一个法向量,且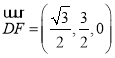
设平面![]() 的法向量
的法向量![]() ,又
,又![]() ,
,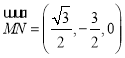
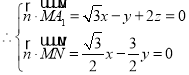 ,令
,令![]() ,则
,则![]() ,
,![]()
![]()
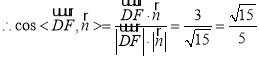
![]()
![]() 二面角
二面角![]() 的正弦值为:
的正弦值为:![]()


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图像相邻的两个对称中心之间的距离为
,其图像相邻的两个对称中心之间的距离为![]() ,且有一条对称轴为直线
,且有一条对称轴为直线![]() ,则下列判断正确的是 ( )
,则下列判断正确的是 ( )
A. 函数![]() 的最小正周期为
的最小正周期为![]()
B. 函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
D. 函数![]() 的图像关于点
的图像关于点![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ex﹣ax2﹣2x+b(e为自然对数的底数,a,b∈R).
(Ⅰ)设f′(x)为f(x)的导函数,证明:当a>0时,f′(x)的最小值小于0;
(Ⅱ)若a<0,f(x)>0恒成立,求符合条件的最小整数b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“?x∈R,2x>0”的否定是“?x0∈R,2 ![]() <0”
<0”
B.命题“若sinx=siny,则x=y”的逆否命题为真命题
C.若命题p,¬q都是真命题,则命题“p∧q”为真命题
D.命题“若△ABC为锐角三角形,则有sinA>cosB”是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F. 
(1)求证:BD⊥AD;
(2)若AC=BD,AB=6,求弦DE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示. 
(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某市供电公司数据,2019年1月份市新能源汽车充电量约270万度,同比2018年增长![]() ,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照
,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照![]() ,
,![]() ,…,
,…,![]() 分成5组,制成如图所示的频率分布直方图.
分成5组,制成如图所示的频率分布直方图.
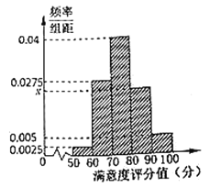
(1)求图中![]() 的值并估计样本数据的中位数;
的值并估计样本数据的中位数;
(2)已知满意度评分值在![]() 内的男女司机人数比为
内的男女司机人数比为![]() ,从中随机抽取2人进行座谈,求2人均为女司机的概率.
,从中随机抽取2人进行座谈,求2人均为女司机的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com