
【题目】已知f(x)=ex﹣ax2﹣2x+b(e为自然对数的底数,a,b∈R).
(Ⅰ)设f′(x)为f(x)的导函数,证明:当a>0时,f′(x)的最小值小于0;
(Ⅱ)若a<0,f(x)>0恒成立,求符合条件的最小整数b.
【答案】解:(Ⅰ)证明:令g(x)=f'(x)=ex﹣2ax﹣2,则g'(x)=ex﹣2a,
因为a>0,令g'(x0)=0,x0=ln2a,
所以当x∈(﹣∞,ln2a)时,g'(x)<0,g(x)单调递减;
当x∈(ln2a,+∞)时,g'(x)>0,g(x)单调递增
则f'(x)min=g(x)min=g(ln2a)=eln2a﹣2aln2a﹣2=2a﹣2aln2a﹣2
令G(x)=x﹣xlnx﹣2,(x>0)G'(x)=1﹣(lnx+1)=﹣lnx当x∈(0,1)时,
G'(x)>0,G(x)单调递增
当x∈(1,+∞)时,G'(x)<0,G(x)单调递减
所以G(x)max=G(1)=﹣1<0,所以f'(x)min<0成立.
(Ⅱ)f(x)>0恒成立,等价于f(x)min>0恒成立
令g(x)=f'(x)=ex﹣2ax﹣2,则g'(x)=ex﹣2a,
因为a<0,所以g'(x)>0,所以g(x)单调递增,
又g(0)=﹣1<0,g(1)=e﹣2a﹣2>0,所以存在x0∈(0,1),使得g(x0)=0
则x∈(﹣∞,x0)时,g(x)=f'(x)<0,f(x)单调递减;
x∈(x0 , +∞)时,g(x)=f'(x)>0,f(x)单调递增;
所以f(x)min=f(x0)=ex0﹣ax02﹣2x0+b>0恒成立…(1)
且ex0﹣2ax0﹣2=0…(2)
由(1)(2), 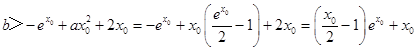 即可
即可
又由(2)a= ![]() <0,所以x0∈(0,ln2)
<0,所以x0∈(0,ln2)
令 ![]() +x,x∈(0,ln2)n(x)=m'(x)=
+x,x∈(0,ln2)n(x)=m'(x)= ![]() +1n'(x)=
+1n'(x)= ![]() >0,
>0,
所以n(x)>n(0)= ![]() >0,所以m(x)单调递增,m(x)>m(0)=(﹣1)e0=﹣1,
>0,所以m(x)单调递增,m(x)>m(0)=(﹣1)e0=﹣1, ![]() +ln2=2ln2﹣2
+ln2=2ln2﹣2
所以b>﹣1,所以符合条件的b=0
法2:令x=0,f(0)=1+b>0,b>﹣1,故符合条件的最小整数b=0.
现证明b=0时,f(x)>0 求f(x)=ex﹣ax2﹣2x的最小值即可
令g(x)=f'(x)=ex﹣2ax﹣2,则g'(x)=ex﹣2a,因为a<0,所以g'(x)>0,所以g(x)单调递增,
又g(0)=﹣1<0,g(1)=e﹣2a﹣2>0,所以存在x0∈(0,1),使得g(x0)=0,
则x∈(﹣∞,x0)时,g(x)=f'(x)<0,f(x)单调递减;
x∈(x0 , +∞)时,g(x)=f'(x)>0,f(x)单调递增;
所以f(x)min=f(x0)=ex0﹣ax02﹣2x0 . (1)
且ex0﹣2ax0﹣2=0…(2)
f(x)min=f(x0)=ex0﹣ ![]()
又由(2)a= ![]() <0,所以x0∈(0,ln2))
<0,所以x0∈(0,ln2))
现在求函数 ![]() ﹣x,x∈(0,ln2)的范围q(x0)=p'(x)=
﹣x,x∈(0,ln2)的范围q(x0)=p'(x)= ![]() ﹣1,q'(x0)=﹣
﹣1,q'(x0)=﹣ ![]() <0,
<0,
所以q(x)<q(0)=﹣ ![]() <0,所以p(x)单调递减,p(x)<p(0)=(﹣1)e0=1
<0,所以p(x)单调递减,p(x)<p(0)=(﹣1)e0=1 ![]() ﹣ln2=2﹣ln2>0
﹣ln2=2﹣ln2>0
所以b=0是符合条件的.
【解析】(Ⅰ)令g(x)=f'(x)=ex﹣2ax﹣2,求出g'(x)=ex﹣2a,判断导函数的符号,推出单调性,求出原函数的导数的最小值,再构造最小值函数,利用导数求解最小值函数的最大值为负值,说明f'(x)min<0成立.(Ⅱ)利用f(x)>0恒成立,等价于f(x)min>0恒成立,构造g(x)=f'(x)=ex﹣2ax﹣2,求出导函数g'(x)=ex﹣2a,判断单调性,推出 ![]() 恒成立且
恒成立且 ![]() 求出b的表达式,a的表达式,在构造函数令
求出b的表达式,a的表达式,在构造函数令 ![]() ,判断单调性,求出满足椭圆的b即可.法2:令x=0,得到符合条件的最小整数b=0,然后证明b=0时,f(x)>0 求f(x)=ex﹣ax2﹣2x的最小值.令g(x)=f'(x)=ex﹣2ax﹣2,判断g(x)单调性,求解函数
,判断单调性,求出满足椭圆的b即可.法2:令x=0,得到符合条件的最小整数b=0,然后证明b=0时,f(x)>0 求f(x)=ex﹣ax2﹣2x的最小值.令g(x)=f'(x)=ex﹣2ax﹣2,判断g(x)单调性,求解函数 ![]() ,且
,且 ![]() ,在构造函数函数
,在构造函数函数 ![]() ,利用函数的最值,推出b=0是符合条件的.
,利用函数的最值,推出b=0是符合条件的.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】统计表明某型号汽车在匀速行驶中每小时的耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数为
(千米/小时)的函数为![]()
![]() .
.
(1)当![]() 千米/小时时,行驶
千米/小时时,行驶![]() 千米耗油量多少升?
千米耗油量多少升?
(2)若油箱有![]() 升油,则该型号汽车最多行驶多少千米?
升油,则该型号汽车最多行驶多少千米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
(Ⅰ)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(Ⅱ)在某场比赛中,考察他前4次投篮命中到篮筐中心的水平距离的情况,并且规定:运动员投篮命中时,他到篮筐中心的水平距离不少于4米的记1分,否则扣掉1分.用随机变量X表示第4次投篮后的总分,将频率视为概率,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从
年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从![]() 年下半年的会员中随机调查了
年下半年的会员中随机调查了![]() 个会员,得到会员对售后服务的满意度评分如下:
个会员,得到会员对售后服务的满意度评分如下:
![]()
根据会员满意度评分,将会员的满意度从低到高分为三个等级:
满意度评分 | 低于 |
| 不低于 |
满意度等级 | 不满意 | 比较满意 | 非常满意 |
(1)根据这![]() 个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
(2)以(1)中的频率作为概率,假设每个会员的评价结果相互独立.
(i)若从下半年的所有会员中随机选取![]() 个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
(ii)若从下半年的所有会员中随机选取![]() 个会员,记评分非常满意的会员的个数为
个会员,记评分非常满意的会员的个数为![]() ,求
,求![]() 的分布列,数学期望
的分布列,数学期望![]() 及方差
及方差![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 截以坐标原点
截以坐标原点![]() 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 切于第一象限,且与坐标轴交于点
切于第一象限,且与坐标轴交于点![]() ,
,![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)设![]() ,
,![]() 是圆
是圆![]() 上任意两点,点
上任意两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,若直线
,若直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() 和
和![]() ,问
,问![]() 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某名校从2008年到2017年考入清华、北大的人数可以通过以下表格反映出来.(为了方便计算,将2008年编号为1,2009年编号为2,以此类推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)根据最近5年的数据,利用最小二乘法求出![]() 与
与![]() 之间的线性回归方程,并用以预测2018年该校考入清华、北大的人数;(结果要求四舍五入至个位)
之间的线性回归方程,并用以预测2018年该校考入清华、北大的人数;(结果要求四舍五入至个位)
(2)从这10年的数据中随机抽取2年,记其中考入清华、北大的人数不少于![]() 的有
的有![]() 年,
年,
求![]() 的分布数列和数学期望.
的分布数列和数学期望.
参考公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b=acosC+3bsin(B+C).
(1)若 ![]() ,求角A;
,求角A;
(2)在(1)的条件下,若△ABC的面积为 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com