
 上的点,以M为圆心的圆与x轴相切于椭圆的焦点F,圆M与y轴相交于P,Q,若△PQM是钝角三角形,则椭圆离心率的取值范围是 .
上的点,以M为圆心的圆与x轴相切于椭圆的焦点F,圆M与y轴相交于P,Q,若△PQM是钝角三角形,则椭圆离心率的取值范围是 . 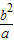 或
或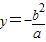 ,所以圆的半径为
,所以圆的半径为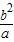 ,过M作MN⊥Y轴与N,则PN=NQ,MN=c,PN=NQ=
,过M作MN⊥Y轴与N,则PN=NQ,MN=c,PN=NQ=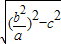 ,由∠PQM为钝角,知
,由∠PQM为钝角,知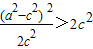 ,由此能够求出椭圆离心率的取值范围.
,由此能够求出椭圆离心率的取值范围.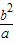 或
或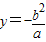 (a2=b2+c2),
(a2=b2+c2),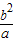 ,
,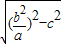 ,
, >c,即
>c,即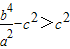 ,
,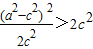 ,
,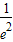 -4+e2>0,
-4+e2>0,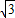 (0<e<1)
(0<e<1)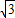 +2
+2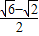 .
.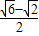 ).
).

 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
| x2 |
| 16 |
| y2 |
| 20 |
| PA |
| PF |
查看答案和解析>>
科目:高中数学 来源:2012届福建省泉州市高三上学期期中文科数学试卷 题型:填空题
M是椭圆 上的点,以M为圆心的圆与x轴相切于椭圆的焦点F,圆M与y轴相交于P,Q。若
上的点,以M为圆心的圆与x轴相切于椭圆的焦点F,圆M与y轴相交于P,Q。若 为钝角三角形,则椭圆的离心率的取值范围为
为钝角三角形,则椭圆的离心率的取值范围为
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市盱眙县新马中学高三(上)第八周内测数学试卷(文科)(解析版) 题型:填空题
 上的点,以M为圆心的圆与x轴相切于椭圆的焦点F,圆M与y轴相交于P,Q,若△PQM是钝角三角形,则椭圆离心率的取值范围是 .
上的点,以M为圆心的圆与x轴相切于椭圆的焦点F,圆M与y轴相交于P,Q,若△PQM是钝角三角形,则椭圆离心率的取值范围是 .查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市盱眙县新马中学高三(上)第八周内测数学试卷(文科)(解析版) 题型:填空题
 上的点,以M为圆心的圆与x轴相切于椭圆的焦点F,圆M与y轴相交于P,Q,若△PQM是钝角三角形,则椭圆离心率的取值范围是 .
上的点,以M为圆心的圆与x轴相切于椭圆的焦点F,圆M与y轴相交于P,Q,若△PQM是钝角三角形,则椭圆离心率的取值范围是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com