【题目】在直线l：3x－y－1＝0上求点P和Q，使得

(1)点P到点A(4,1)和B(0,4)的距离之差最大；

(2)点Q到点A(4,1)和C(3,4)的距离之和最小．

参考答案：

【答案】（1）P(2,5)； （2）Q．

【解析】

(1)设点B关于l的对称点B′的坐标为(a，b)，求得B′的坐标，进一步可得直线AB′的方程，联立直线方程即可求得点P的坐标.

(2)设点C关于l的对称点为C′，求得C′的坐标，进一步可得直线AC′的方程，联立直线方程即可求得点Q的坐标.

(1)如图所示，设点B关于l的对称点B′的坐标为(a，b)，

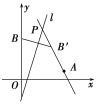
则kBB′·k1＝－1，

即3× ，

∴a＋3b－12＝0.①

线段BB′的中点坐标为，且中点在直线l上，

∴3×－1＝0，即3a－b－6＝0.②

解①②得a＝3，b＝3，∴B′(3,3)．

于是直线AB′的方程为，即2x＋y－9＝0．

解得 即l与直线AB′的交点坐标为P(2,5)，且此时点P到点A，B的距离之差最大．

(2)如图所示，设点C关于l的对称点为C′，

求出C′的坐标为 ．

∴AC′所在直线的方程为19x＋17y－93＝0，

解得直线AC′和l交点坐标为，

故Q点坐标为，且此时点P到点A，C的距离之和最小．

关闭