
【题目】如图1,在路边安装路灯,路宽为![]() ,灯柱
,灯柱![]() 长为
长为![]() 米,灯杆
米,灯杆![]() 长为1米,且灯杆与灯柱成
长为1米,且灯杆与灯柱成![]() 角,路灯采用圆锥形灯罩,其轴截面的顶角为
角,路灯采用圆锥形灯罩,其轴截面的顶角为![]() ,灯罩轴线
,灯罩轴线![]() 与灯杆
与灯杆![]() 垂直.
垂直.
⑴设灯罩轴线与路面的交点为![]() ,若
,若![]() 米,求灯柱
米,求灯柱![]() 长;
长;
⑵设![]() 米,若灯罩截面的两条母线所在直线一条恰好经过点
米,若灯罩截面的两条母线所在直线一条恰好经过点![]() ,另一条与地面的交点为
,另一条与地面的交点为![]() (如图2)
(如图2)


(图1) (图2)
(ⅰ)求![]() 的值;(ⅱ)求该路灯照在路面上的宽度
的值;(ⅱ)求该路灯照在路面上的宽度![]() 的长.
的长.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
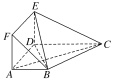
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
, ![]() ,
, ![]() ,若
,若![]() 为
为![]() 的中点,且
的中点,且![]() .
.
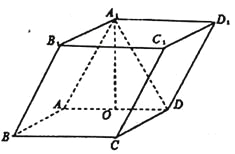
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9 元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85(元/km)).
(1)将某乘客搭乘一次出租车的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16 km,他准备先乘一辆出租车行驶8 km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?
(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.
(Ⅰ)求{an}的通项公式an与前n项和公式Sn;
(Ⅱ)令bn=![]() (k<0),若{bn}是等差数列,求数列{
(k<0),若{bn}是等差数列,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com