
【题目】在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
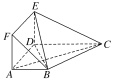
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
【答案】见解析
【解析】
解:(1)证明:因为AD=1,CD=2,AC=![]() ,
,
所以AD2+CD2=AC2,
所以△ADC为直角三角形,且AD⊥DC.
同理,因为ED=1,CD=2,EC=![]() ,
,
所以ED2+CD2=EC2,
所以△EDC为直角三角形,且ED⊥DC.
又四边形ADEF是正方形,所以AD⊥DE,
又AD∩DC=D,所以ED⊥平面ABCD.
又BC平面ABCD,所以ED⊥BC.
在梯形ABCD中,过点B作BH⊥CD于点H,
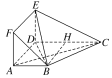
故四边形ABHD是正方形,所以∠ADB=45°,BD=![]() 。
。
在Rt△BCH中,BH=CH=1,所以BC=![]() ,
,
故BD2+BC2=DC2,所以BC⊥BD.
因为BD∩ED=D,BD平面EBD,ED平面EBD,
所以BC⊥平面EBD,
又BC平面EBC,所以平面EBC⊥平面EBD.
(2)在线段BC上存在一点T,使得MT∥平面BDE,此时3BT=BC.
连接MT,在△EBC中,因为![]() =
=![]() =
=![]() ,所以MT∥EB.
,所以MT∥EB.
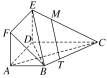
又MT平面BDE,EB平面BDE,
所以MT∥平面BDE。


科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点,焦点在![]() 轴上的椭圆,离心率为
轴上的椭圆,离心率为![]() 且过点
且过点![]() ,过定点
,过定点![]() 的动直线与该椭圆相交于
的动直线与该椭圆相交于![]() 、
、![]() 两点.
两点.
(1)若线段![]() 中点的横坐标是
中点的横坐标是![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx为偶函数,数列{an}满足an+1=2f(an-1)+1,且a1=3,an>1.
(1)设bn=log2(an-1),证明:数列{bn+1}为等比数列;
(2)设cn=nbn,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
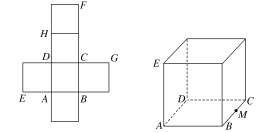
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当|OP|=|OM|时,求l的方程及△POM的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有10个著名景点,其中8 个为日游景点,2个为夜游景点.某旅行团要从这10个景点中选5个作为二日游的旅游地.行程安排为第一天上午、下午、晚上各一个景点,第二天上午、下午各一个景点.
(1)甲、乙两个日游景点至少选1个的不同排法有多少种?
(2)甲、乙两日游景点在同一天游玩的不同排法有多少种?
(3)甲、乙两日游景点不同时被选,共有多少种不同排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在路边安装路灯,路宽为![]() ,灯柱
,灯柱![]() 长为
长为![]() 米,灯杆
米,灯杆![]() 长为1米,且灯杆与灯柱成
长为1米,且灯杆与灯柱成![]() 角,路灯采用圆锥形灯罩,其轴截面的顶角为
角,路灯采用圆锥形灯罩,其轴截面的顶角为![]() ,灯罩轴线
,灯罩轴线![]() 与灯杆
与灯杆![]() 垂直.
垂直.
⑴设灯罩轴线与路面的交点为![]() ,若
,若![]() 米,求灯柱
米,求灯柱![]() 长;
长;
⑵设![]() 米,若灯罩截面的两条母线所在直线一条恰好经过点
米,若灯罩截面的两条母线所在直线一条恰好经过点![]() ,另一条与地面的交点为
,另一条与地面的交点为![]() (如图2)
(如图2)


(图1) (图2)
(ⅰ)求![]() 的值;(ⅱ)求该路灯照在路面上的宽度
的值;(ⅱ)求该路灯照在路面上的宽度![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com