Question

已知a,b是两个非零向量，同时满足|a|=|b|=|a-b|，求a与a+b的夹角.

Answer 1

解法一：根据|a|=|b|，有|a|²=|b|²，

又由|b|=|a-b|，得|b|²=|a|²-2a·b+|b|²，

∴a·b=|a|².

而|a+b|²=|a|²+2a·b+|b|²=3|a|²,

∴|a+b|=.

设a与a+b的夹角为θ，则

cosθ=，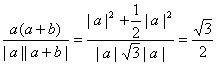

∴θ=30°.

解法二：设向量a=(x₁,y₁)，b=(x₂,y₂)，

∵|a|=|b|,∴.

由|b|=|a-b|，得x₁x₂+y₁y₂=(),即a·b=().

由|a+b|²=2()+2×()=3()，得|a+b|=().

设a与a+b的夹角为θ，则cosθ=，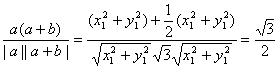

∴θ=30°.

解法三：根据向量加法的几何意义，在平面内任取一点O，作=a，OB=b，以OA、OB为邻边作平行四边形OACB.

∵|a|=|b|，即||=||，∴OACB为菱形，OC平分∠AOB，这时=a+b，=a-b.而|a|=|b|=|a-b|，即||=||=||.

∴△AOB为正三角形，则∠AOB=60°，于是∠AOC=30°，即a与a+b的夹角为30°.