
 ,从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为
,从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为 ;若前次出现绿球,则下一次出现红球、绿球的概率分别为
;若前次出现绿球,则下一次出现红球、绿球的概率分别为 ,记第n次按下按钮后出现红球的概率为Pn.
,记第n次按下按钮后出现红球的概率为Pn.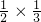 =
= ,
,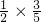 =
= ,
, +
+ =
=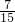 .
. ,
, ,
, +
+ (1-Pn-1 )=
(1-Pn-1 )= -
- Pn-1,即Pn=
Pn-1,即Pn= -
- Pn-1,n∈N,n≥2.
Pn-1,n∈N,n≥2. (Pn-1+x),即 Pn=-
(Pn-1+x),即 Pn=- Pn-1-
Pn-1- .
. =
= ,解得 x=
,解得 x= ,∴Pn-
,∴Pn-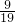 =-
=- (Pn-1-
(Pn-1-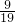 ),
),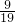 }是等比数列,首项等于
}是等比数列,首项等于 =
= ,公比等于-
,公比等于- .
. =
=
 ,∴Pn=
,∴Pn=
 +
+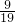 .
.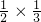 ,第一次出现绿球,第二次出现红球的概率为:
,第一次出现绿球,第二次出现红球的概率为: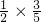 ,相加即得所求.
,相加即得所求. +
+ (1-Pn-1 )化简求得结果.
(1-Pn-1 )化简求得结果. (Pn-1+x),即 Pn=-
(Pn-1+x),即 Pn=- Pn-1-
Pn-1- . 令-
. 令- =
= ,解得 x=
,解得 x= ,故Pn-
,故Pn-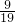 =-
=- (Pn-1-
(Pn-1-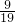 ),故{ Pn-
),故{ Pn-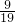 }是等比数列,首项等于
}是等比数列,首项等于 =
= ,公比等于-
,公比等于- ,由此求得Pn关于n的表达式.
,由此求得Pn关于n的表达式.

 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求P2的值;
(2)当n∈N且n≥2时,求用Pn-1表示Pn的表达式.
(3)求Pn关于n的表达式.
查看答案和解析>>
科目:高中数学 来源:2012年湖南省湘潭市高考数学三模试卷(理科)(解析版) 题型:解答题
 ,从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为
,从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为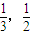 ;若前次出现绿球,则下一次出现红球、绿球的概率分别为
;若前次出现绿球,则下一次出现红球、绿球的概率分别为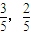 ,记第n次按下按钮后出现红球的概率为Pn.
,记第n次按下按钮后出现红球的概率为Pn.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com