Question

（20）某城市2001年末汽车保有量为30万辆，预计此后每年报废上一年末汽车保有量的6%，并且每年新增汽车数量相同.为保护城市环境，要求该城市汽车保有量不超过60万辆，那么每年新增汽车数量不应超过多少辆?

Answer 1

（20）本小题主要考查数列、数列的极限等基础知识，考查建立数学模型、运用所学知识解决实际问题的能力.

解：设2001年末汽车保有量为b₁万辆，以后各年末汽车保有量依次为b₂万辆，b₃万辆，…，每年新增

汽车x万辆，则b₁＝30，b₂＝b₁×0.94＋x. 　　　　　　 　　　　　　　　

对于n＞1，有

b_n＋1 ＝b_n×0.94＋x

＝b_n－1×0.94²＋（1＋0.94）x，

……

∴b_n＋1 ＝b₁×0.94ⁿ＋x（1＋0.94＋…＋0.94^n－1）

 

＝b₁×0.94ⁿ＋x

 

＝＋（30－）×0.94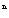　　　　　　　　　　

 

当30－≥0，即x≤1.８时，b_n＋1≤b_n≤…≤b₁＝30.　　　　　　　　　　　　　　　　　

当30－＜0，即x＞1.8时，

 

b_n＝［＋（30－）×0.94^n－1］＝，

 

并且数列｛b_n｝逐项增加，可以任意靠近.　　　　　　　　

 

因此，如果要求汽车保有量不超过60万辆，即b_n≤60（n＝1，2，3，…）.

则≤60，即x≤3.6（万辆）.

综上，每年新增汽车不应超过3.6万辆.