
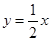 上时,求直线AB的方程.
上时,求直线AB的方程.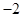 ;(2)
;(2)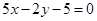
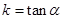 求斜率,二是求出直线上两点坐标,利用斜率公式
求斜率,二是求出直线上两点坐标,利用斜率公式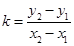 求斜率。本题属于第二种方法,应先设出A,B两点坐标,根据中点坐标公式求出A,B两点,再代入公式求斜率。(2)因为已知直线AB过点P,则可用点斜式求直线AB的方程,故可设其方程为
求斜率。本题属于第二种方法,应先设出A,B两点坐标,根据中点坐标公式求出A,B两点,再代入公式求斜率。(2)因为已知直线AB过点P,则可用点斜式求直线AB的方程,故可设其方程为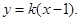 ,但需注意讨论斜率不存在时的情况。解两个方程组可求得点A,点B的坐标,利用中点坐标公式求出中点再代入
,但需注意讨论斜率不存在时的情况。解两个方程组可求得点A,点B的坐标,利用中点坐标公式求出中点再代入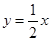 ,可解出K.
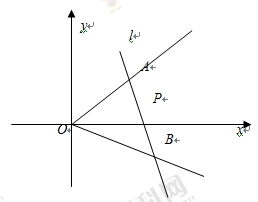
,可解出K.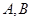 分别为直线与射线
分别为直线与射线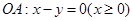 及
及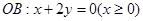 的交点,
的交点, 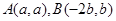 ,又点
,又点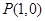 是
是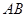 的中点,所以有
的中点,所以有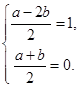 即
即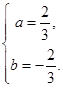
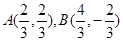 ,
,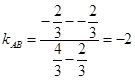 ,
,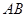 的斜率不存在时,则
的斜率不存在时,则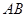 的方程为
的方程为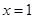 ,易知
,易知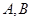 两点的坐标分别为
两点的坐标分别为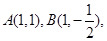 所以
所以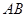 的中点坐标为
的中点坐标为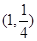 ,显然不在直线
,显然不在直线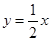 上,
上,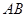 的斜率不存在时不满足条件.
的斜率不存在时不满足条件. 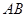 的斜率存在时,记为
的斜率存在时,记为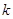 ,易知
,易知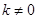 且
且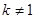 ,则直线
,则直线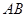 的方程为
的方程为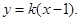
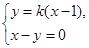 及
及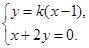
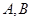 两点的坐标分别为
两点的坐标分别为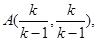
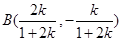
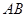 的中点坐标为
的中点坐标为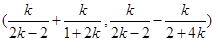 .
.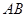 的中点在直线
的中点在直线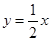 上,
上,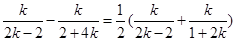 ,
,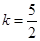 .
.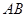 的方程为
的方程为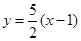 ,
,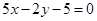 .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com