
分析 从圆M上的点向圆上的点连线成角,当且仅当两条线均为切线时才是最大的角,OP=1,利用圆O和圆M上分别存在点P,Q,使得∠OQP=30°,可得|OM|≤2,进而得出答案.
解答 解:由题意,圆M:(x+a+3)2+(y-2a)2=1(a为实数),圆心为M(-a-3,2a)
从圆M上的点向圆上的点连线成角,当且仅当两条线均为切线时才是最大的角,OP=1.
∵圆O和圆M上分别存在点P,Q,使得∠OQP=30°,
∴|OM|≤2,
∴(a+3)2+4a2≤4,
∴-1≤a≤$\frac{3}{5}$,
故答案为:-1≤a≤$\frac{3}{5}$.
点评 本题考查了直线与圆相切的性质、两点间的距离的计算公式、数形结合思想方法,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
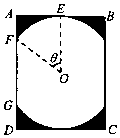 某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m且$\frac{AB}{AD}$≥$\frac{1}{2}$,设∠EOF=θ,透光区域的面积为S.
某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m且$\frac{AB}{AD}$≥$\frac{1}{2}$,设∠EOF=θ,透光区域的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
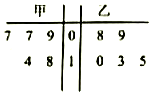 如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.
如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{3}$ | C. | $\frac{11}{3}$ | D. | -1或$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 10 | 30 | 30 | 20 | 5 | 5 |
| 赞成人数 | 8 | 25 | 24 | 10 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com