解:(1)由题意设椭圆C的标准方程是

,
由题意知
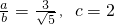
,又因a
2=b
2+c
2,
解得a
2=9,b
2=5,
∴椭圆C的标准方程为
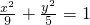
.
(2)设P(x
0,y
0),∵A(-3,0),B(3,0),
∴直线

,
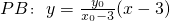
令x=0,分别代入上面的直线方程得:M(0,

),N(0,

),
∴
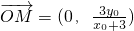
,

,
∴

=

•

=5.
(3)∵
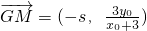
,
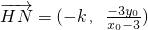
又∵
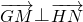
,∴

,
∴两正方形的面积和为
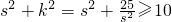
当且仅当s
2=k
2=5时,等式成立,
∴两正方形的面积和的最小值为10,此时G
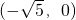
、H
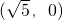
.
分析:(1)由题意设出椭圆方程,由条件和a
2=b
2+c
2求出a
2和b
2的值;
(2)设出点P的坐标和点A和B坐标,求出直线PA和PB的方程,令x=0求出点M和N坐标,即求出

的坐标,由向量的数量积运算求出

,根据点P在椭圆上求出值;
(3)由(2)求出点M和N坐标以及题意求出

,根据向量数量积运算和
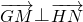
求出关于sk的积,再由基本不等式求出面积的最小值,注意等号成立的条件,进而求出G、H点坐标.
点评:本题考查了椭圆方程的求法以及椭圆的性质、向量数量积的几何意义,利用a、b、c、e几何意义和a
2=b
2+c
2求出a和b的值,根据椭圆上点的坐标满足方程求出数量积的值,根据基本不等式和条件求出最值,注意“一正二定三相等”的利用,此题综合性强,涉及的知识多,考查了分析问题和解决问题的能力.

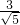 ,焦点坐标分别为F1(-2,0),F2(2,0).
,焦点坐标分别为F1(-2,0),F2(2,0). 的值;
的值;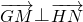 ,(s<k),分别以OG、OH为边作两正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标.
,(s<k),分别以OG、OH为边作两正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标. ,
,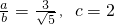 ,又因a2=b2+c2,
,又因a2=b2+c2,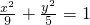 .
. ,
,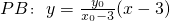
 ),N(0,
),N(0, ),
),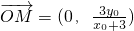 ,
, ,
, =
= •
• =5.
=5.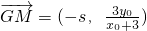 ,
,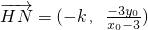
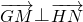 ,∴
,∴ ,
,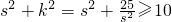
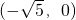 、H
、H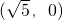 .
. 的坐标,由向量的数量积运算求出
的坐标,由向量的数量积运算求出 ,根据点P在椭圆上求出值;
,根据点P在椭圆上求出值; ,根据向量数量积运算和
,根据向量数量积运算和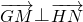 求出关于sk的积,再由基本不等式求出面积的最小值,注意等号成立的条件,进而求出G、H点坐标.
求出关于sk的积,再由基本不等式求出面积的最小值,注意等号成立的条件,进而求出G、H点坐标.

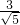 ,焦点坐标分别为F1(-2,0),F2(2,0).
,焦点坐标分别为F1(-2,0),F2(2,0).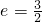 的双曲线的标准方程.
的双曲线的标准方程.