
(本小题满分9分)
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=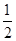 .
.
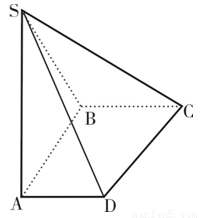
(1)求四棱锥S-ABCD的体积.
(2)求证:面SAB⊥面SBC.
(3)求SC与底面ABCD所成角的正切值.
证明:(1) VS-ABCD=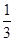 ×
×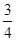 ×1=
×1=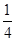 ;(2)见解析;(3)tan∠SCA=
;(2)见解析;(3)tan∠SCA=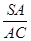 =
= =
=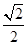 。
。
【解析】(1)根据梯形的面积公式及四棱锥的体积公式直接求值即可.
(2)先由SA⊥面ABCD,可得SA⊥BC,再由AB⊥BC ,得BC⊥平面SAB,从而证得平面SAB⊥平面SBC.
(3)找到线面角是解决问题的关键.连接AC ∵SA⊥面ABCD
∴∠SCA为SC与底面ABCD所成的角,然后解三角形即可.
证明:(1)S梯形ABCD= (AD+BC)·AB=
(AD+BC)·AB= (
( +1)×1=
+1)×1=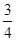
VS-ABCD=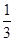 ×
×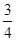 ×1=
×1=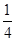 ……………2分
……………2分
(2)∵SA⊥面ABCD ∴SA⊥BC……………………………………3分
又AB⊥BC ∴BC⊥平面SAB
∴平面SAB⊥平面SBC……………………………………5分
(3)连接AC ∵SA⊥面ABCD
∴∠SCA为SC与底面ABCD所成的角……………………………………7分
在Rt△ABC中,AC=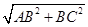 =
=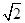
在Rt△SAC中,tan∠SCA=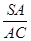 =
= =
=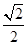 ……………………………………9分
……………………………………9分


科目:高中数学 来源:2010-2011学年北京市东城区高二下学期期末考试文科数学 题型:解答题
(本小题满分9分)
已知 ,且
,且 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)若在数列 中,
中, ,
, ,计算
,计算 ,并由此猜想通项公式
,并由此猜想通项公式 ;
;
(Ⅲ)证明(Ⅱ)中的猜想。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年新疆乌鲁木齐一中高三第一次月考文科数学试卷 题型:解答题
(本小题满分9分)设三角形 的内角
的内角 的对边分别为
的对边分别为
 ,
,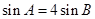 .
.
(1)求 边的长;
边的长;
(2)求角 的大小;
的大小;
(3)求三角形 的面积
的面积 。
。
查看答案和解析>>
科目:高中数学 来源:2010-2011年湖南省衡阳市高一下学期期中考试数学 题型:解答题
.(本小题满分9分)
已知 ,
, 是同一平面内的两个向量,其中
是同一平面内的两个向量,其中 ,
, 且
且 与
与 垂直,(1)求
垂直,(1)求 ;
;
(2)求| -
-  |.
|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com