
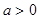 ,两个函数
,两个函数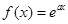 ,
, 的图像关于直线
的图像关于直线 对称.
对称.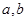 满足的关系式;
满足的关系式;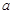 取何值时,函数
取何值时,函数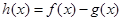 有且只有一个零点;
有且只有一个零点;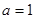 时,在
时,在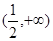 上解不等式
上解不等式 .
.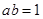 ;(2)
;(2)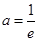 ;(3)
;(3)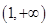 .
.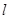 对称,一般都是设
对称,一般都是设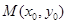 是一个函数图象上的任一点,求出这个点
是一个函数图象上的任一点,求出这个点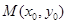 关于直线
关于直线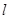 对称的点
对称的点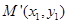 ,而点
,而点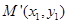 就在第二个函数的图象上,这样就把两个函数建立了联系;(2)函数
就在第二个函数的图象上,这样就把两个函数建立了联系;(2)函数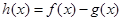 有且只有一个零点,一般是求
有且只有一个零点,一般是求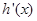 ,通过
,通过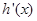 讨论函数
讨论函数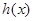 的单调性,最值,从而讨论零点的个数,当然本题中由于
的单调性,最值,从而讨论零点的个数,当然本题中由于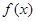 与
与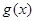 的图象关于直线
的图象关于直线 对称,因此
对称,因此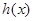 的唯一零点也就是它们的的唯一交点必在直线
的唯一零点也就是它们的的唯一交点必在直线 上,这个交点是函数
上,这个交点是函数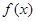 图象与直线
图象与直线 的切点,这样我们可从切线方面来解决问题;(3)考虑
的切点,这样我们可从切线方面来解决问题;(3)考虑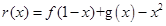
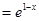
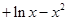 ,
,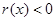 ,还需求
,还需求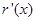 ,讨论
,讨论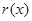 的单调性,极值,从而确定不等式的解集.
的单调性,极值,从而确定不等式的解集.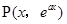 是函数
是函数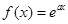 图像上任一点,则它关于直线
图像上任一点,则它关于直线 对称的点
对称的点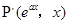 在函数
在函数 的图像上,
的图像上,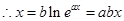 ,
,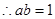 .
.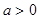 时,函数
时,函数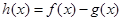 有且只有一个零点,两个函数的图像有且只有一个交点,
有且只有一个零点,两个函数的图像有且只有一个交点,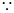 两个函数关于直线
两个函数关于直线 对称,
对称,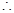 两个函数图像的交点就是函数
两个函数图像的交点就是函数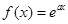 ,的图像与直线
,的图像与直线 的切点.
的切点. ,
,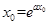
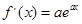 ,
,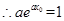 ,
,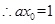 ,
,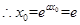 ,
,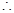 当
当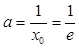 时,函数
时,函数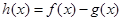 有且只有一个零点
有且只有一个零点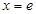 ;
;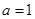 时,设
时,设 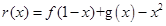
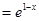
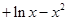 ,则
,则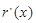
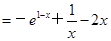 ,当
,当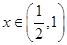 时,
时,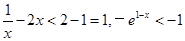 ,
,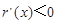 ,
,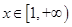 时,
时,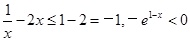 ,
,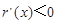 .
.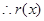 在
在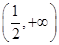 上是减函数.
上是减函数.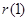 =0,
=0,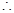 不等式
不等式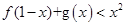 解集是
解集是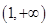 .
.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:不详 题型:单选题
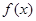 是偶函数,它在[0,+∞)上是减函数.若
是偶函数,它在[0,+∞)上是减函数.若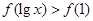 ,则x的取值范围是( )
,则x的取值范围是( )A.( ,1) ,1) | B.(0, )∪(1,+∞) )∪(1,+∞) |
C.( ,10) ,10) | D.(0,1)∪(10,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com