【题目】如图，在棱长为a的正方体ABCD﹣A1B1C1D1中，P为A1D1的中点，Q为A1B1上任意一点，E、F为CD上两点，且EF的长为定值，则下面四个值中不是定值的是（ ）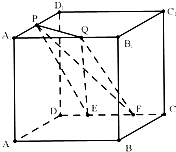 
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.△QEF的面积
【答案】B
【解析】解：A．∵平面QEF即为对角面A1B1CD，点P为A1D1的中点，∴点P到平面QEF即到对角面A1B1CD的距离= 
为定值；
D．∵点Q到直线CD的距离是定值 
a，|EF|为定值，∴△QEF的面积= 
为定值；
C．由A．D可知：三棱锥P﹣QEF的体积为定值；
B．直线PQ与平面PEF所成的角与点Q的位置有关系，因此不是定值，或用排除法即可得出．
综上可得：只有B中的值不是定值．
故选：B．
A．由于平面QEF即为对角面A1B1CD，点P为A1D1的中点，可得：点P到平面QEF即到对角面A1B1CD的距离= 为定值；
D．由于点Q到直线CD的距离是定值 a，|EF|为定值，因此△QEF的面积= 为定值；
C．由A．D可知：三棱锥P﹣QEF的体积为定值；
B．用排除法即可得出．
科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
+ 
=1（a＞b＞0）的左、右焦点分别为F1、F2 ， 点M（0，2）关于直线y=﹣x的对称点在椭圆C上，且△MF1F2为正三角形．
（1）求椭圆C的方程；
（2）垂直于x轴的直线与椭圆C交于A，B两点，过点P（4，0）的直线PB交椭圆C于另一点E，证明：直线AE与x轴相交于定点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设A，B是非空的集合，如果按某一个确定的对应关系f，使对于集合A中的任意一个元素x，在集合中B都有唯一确定的元素y与之对应，那么就称对应f：A→B为从集合A到集合B的一个映射，设f：x→ 
是从集合A到集合B的一个映射．①若A={0，1，2}，则A∩B=；②若B={1，2}，则A∩B= ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆E： 
过点 
，离心率为 
，点F1 ， F2分别为其左、右焦点．
（1）求椭圆E的标准方程；
（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点P，Q，且 
？若存在，求出该圆的方程，并求|PQ|的最大值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆和双曲线焦点F1 ， F2相同，且离心率互为倒数，P是椭圆和双曲线在第一象限的交点，当∠F1PF2=60°时，椭圆的离心率为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知平行四边形ABCD（如图1），AB=4，AD=2，∠DAB=60°，E为AB的中点，把三角形ADE沿DE折起至A1DE位置，使得A1C=4，F是线段A1C的中点（如图2）．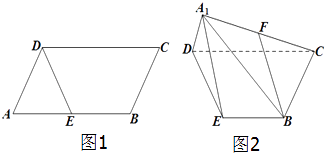 
（1）求证：BF∥面A1DE；
（2）求证：面A1DE⊥面DEBC；
（3）求二面角A1﹣DC﹣E的正切值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图． 
（1）根据茎叶图判断哪个班的平均身高较高；
（2）计算甲班的样本方差；
（3）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
