练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    试求棱长为4a的正八面体二面角的大小及其两条异面棱间的距离．
    分析：设正八面体的棱长为4a，以中心O为原点，对角线DB、AC、QP为x轴、y轴、z轴建立空间直角坐标系，则A（0，-2
    		2
    a，0）、B（2
    		2
    a，0，0）、C（0，2
    		2
    a，0）、P（0，0，2
    		2
    a），设E为BC的中点，连接PE、QE、OE，则∠PEQ=2∠PEO即为所求二面角的平面角；设n=（x，y，z）是AB与PC的公垂线的一个方向向量，则有n•
    AB
    =x+y=0，n•
    PC
    =y-z=0，解得n=（-1，1，1），所以向量
    BC
    =（-2
    		2
    a，2
    		2
    a，0）在n上的射影长d=
    |n•
    BC
    |
    		3
    =
    4
    		6
    a
    3
    即为所求．
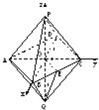
    解答：精英家教网解：如图，设正八面体的棱长为4a，以中心O为原点，
    对角线DB、AC、QP为x轴、y轴、z轴建立空间直角坐标系，
    则A（0，-2
    		2
    a，0）、B（2
    		2
    a，0，0）、C（0，2
    		2
    a，0）、
    P（0，0，2
    		2
    a），设E为BC的中点，连接PE、QE、OE，
    则∠PEQ=2∠PEO即为所求二面角的平面角，∵OE=2a，OP=2
    		2
    a，
    ∴tan∠PEO=
    		2
    ，∠PEQ=2arctan
    		2
    ．
    设n=（x，y，z）是AB与PC的公垂线的一个方向向量，
    则有n•
    AB
    =x+y=0，n•
    PC
    =y-z=0，解得n=（-1，1，1），
    所以向量
    BC
    =（-2
    		2
    a，2
    		2
    a，0）在n上的射影长d=
    |n•
    BC
    |
    		3
    =
    4
    		6
    a
    3
    即为所求．
    点评：本小题主要考查正八面体、棱锥的结构特征，二面角和线面关系等基本知识，同时考查空间想象能力和推理、运算能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2006年高考第一轮复习数学：9.11 多面体与正多面体（解析版） 题型：解答题

    试求棱长为4a的正八面体二面角的大小及其两条异面棱间的距离．

    查看答案和解析>>

    同步练习册答案