
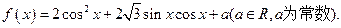
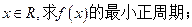
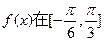 的最大值和最小值和为3,求
的最大值和最小值和为3,求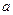 的值.
的值. 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
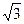 cos2x-2.
cos2x-2.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (米)是时间
(米)是时间 (
( ,单位:时)的函数,记作
,单位:时)的函数,记作 ,下面是某日水深的数据:
,下面是某日水深的数据: (时) (时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
 (米) (米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
 的曲线可以近似地看成函数
的曲线可以近似地看成函数 .
. 的最小正周期、振幅和表达式;
的最小正周期、振幅和表达式; 米或
米或 米以上时认为安全的(船舶停靠时,船底只须不碰海底即可).某船吃水深度(船底离水面的距离)为
米以上时认为安全的(船舶停靠时,船底只须不碰海底即可).某船吃水深度(船底离水面的距离)为 米.如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长
米.如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
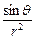 ,其中k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?
,其中k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?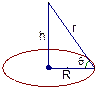
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
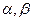 为锐角且
为锐角且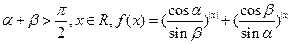
A.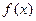 在定义域上为递增函数 在定义域上为递增函数 |
B.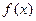 在定义域上为递减函数 在定义域上为递减函数 |
C.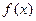 在 在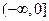 上为增函数,在 上为增函数,在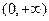 上为减函数 上为减函数 |
D.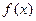 在 在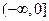 上为减函数,在 上为减函数,在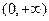 上为增函数 上为增函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com