
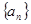 中,
中,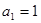 ,
,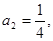 且
且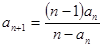
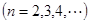 .
.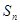 为数列
为数列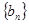 的前
的前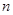 项和,且
项和,且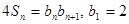
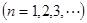 .
.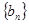 的通项公式;
的通项公式;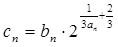 ,求数列
,求数列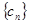 的前
的前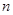 项的和
项的和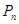 ;
;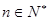 ,有
,有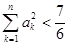 .
.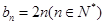 ;(2)
;(2)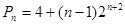 ;(3)证明过程详见解析.
;(3)证明过程详见解析.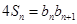 中的n,得到一个等式,2个等式相减,得到
中的n,得到一个等式,2个等式相减,得到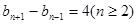 ,分n为奇数偶数进行讨论,分别求出
,分n为奇数偶数进行讨论,分别求出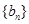 的通项公式,由于得到的式子相同,所以
的通项公式,由于得到的式子相同,所以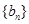 的通项公式就是
的通项公式就是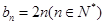 ;第二问,要求数列
;第二问,要求数列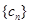 的前n项和,关键是需要求出
的前n项和,关键是需要求出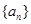 的通项公式,可以利用已知的递推公式进行推导,也可以利用数学归纳法猜想证明,得到
的通项公式,可以利用已知的递推公式进行推导,也可以利用数学归纳法猜想证明,得到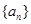 的通项公式后,代入到
的通项公式后,代入到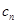 中,得到
中,得到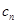 的通项公式,最后用错位相减法进行求和;第三问,先用放缩法对原式进行变形,再用裂项相消法求和,最后和
的通项公式,最后用错位相减法进行求和;第三问,先用放缩法对原式进行变形,再用裂项相消法求和,最后和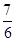 作比较.
作比较.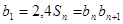 得
得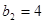 ,
, ,
,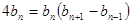 ,
,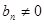 ,即
,即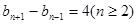 ,当n为奇数时,
,当n为奇数时,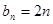 ;当n为偶数时,
;当n为偶数时,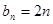 .
.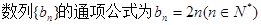 .4分
.4分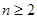 有
有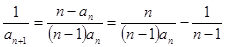 ,
,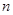 ,得
,得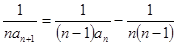 ,即
,即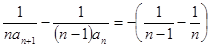 ,
,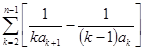 =
=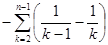 =
=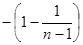 ,
,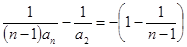 ,
,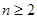 ,所以
,所以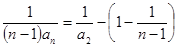 =
=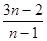 ,
,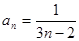 ,
,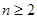 ,又
,又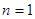 时也成立,故
时也成立,故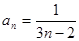 ,
,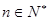 .
.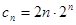 ,
,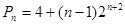 8分
8分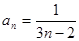 ,然后用数学归纳法证明.
,然后用数学归纳法证明.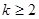 ,有
,有 ,
,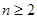 时,有
时,有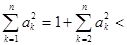
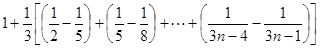
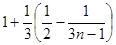
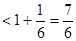 .
.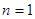 时,
时,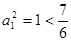 .故对一切
.故对一切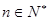 ,有
,有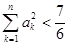 .14分
.14分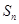 求
求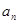 ;2.错位相减法;3.数学归纳法;4.裂项相消法.
;2.错位相减法;3.数学归纳法;4.裂项相消法.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com