
分析 根据特征多项式的一个零点为-2,可得x的值,即可求得矩阵M,利用矩阵的乘法即可得解M2的值.
解答 解:∵λ=-2代入$|{\begin{array}{l}{λ+1}&{-2}\\{-\frac{5}{2}}&{λ-x}\end{array}}|={λ^2}-(x-1)λ-(x+5)=0$,得x=3,
∴矩阵$M=[{\begin{array}{l}{-1}&2\\{\frac{5}{2}}&3\end{array}}]$,…(5分)
∴${M^2}=[{\begin{array}{l}6&4\\ 5&{14}\end{array}}]$.…(10分)
点评 本题给出含有字母参数的矩阵,在知其一个特征值的情况下求矩阵,考查了特征值与特征向量的计算的知识,属于基础题.


科目:高中数学 来源: 题型:解答题
 某校从高一年级A,B两个班中各选出7名学生参加物理竞赛,他们的成绩(单位:分)的茎叶图如图所示,其中A班学生的平均分是85分
某校从高一年级A,B两个班中各选出7名学生参加物理竞赛,他们的成绩(单位:分)的茎叶图如图所示,其中A班学生的平均分是85分查看答案和解析>>
科目:高中数学 来源: 题型:填空题
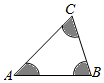 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
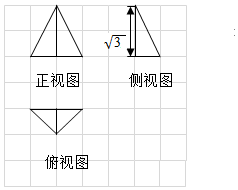 网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )
网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
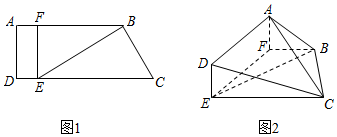 如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2).
如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
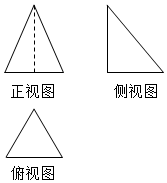 已知三棱锥的三视图的正视图是等腰三角形,俯视图是边长为$\sqrt{3}$的等边三角形,侧视图是等腰直角三角形,则三棱锥的四个面中面积的最大值为为$\frac{3\sqrt{6}}{4}$.
已知三棱锥的三视图的正视图是等腰三角形,俯视图是边长为$\sqrt{3}$的等边三角形,侧视图是等腰直角三角形,则三棱锥的四个面中面积的最大值为为$\frac{3\sqrt{6}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com