Question

17．如图，在三棱柱ABC-A₁B₁C₁中，侧棱A₁A⊥平面ABC，AC⊥BC，AC=1，BC=2，S，点D是AB的中点．
（I）证明：AC₁∥平面CDB₁；
（Ⅱ）在线段AB上找一点P，使得直线AC₁与CP所成角的为60°，求$\frac{{|{\overrightarrow{AP}}|}}{{|{\overrightarrow{AB}}|}}$的值．

Answer 1

分析 （Ⅰ）设CB₁与C₁B相交于E，连结DE，证明DE∥AC₁，然后证明AC₁∥平面CDB₁．
（Ⅱ）建立空间直角坐标系，CC₁为z轴，CA为x轴，CB为y轴，设$\overrightarrow{AP}=λ\overrightarrow{AB}（0＜λ＜1）$，利用向量的数量积转化求解即可．

解答 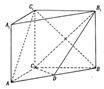（Ⅰ）证明：设CB₁与C₁B相交于E，连结DE，…．（2分）
∵D是AB的中点，E是BC₁的中点，∴DE∥AC₁，…．（6分）
∵DE?平面CDB₁，AC₁?平面CDB₁，
∴AC₁∥平面CDB₁．…．（7分）
（Ⅱ）建立空间直角坐标系，CC₁为z轴，CA为x轴，CB为y轴，…．（9分）
设$\overrightarrow{AP}=λ\overrightarrow{AB}（0＜λ＜1）$，
$\overrightarrow{CP}=\overrightarrow{CA}+λ\overrightarrow{AB}=（{1-λ，2λ，0}）$，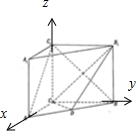
$\overrightarrow{A{C_1}}=（{-1，0，1}）$
所以$|{cos\left?{\overrightarrow{A{C_1}}，\overrightarrow{CP}}\right＞}|=\frac{1}{2}$$⇒λ=\frac{1}{3}$
即求$\frac{{|{\overrightarrow{AP}}|}}{{|{\overrightarrow{AB}}|}}$=$\frac{1}{3}$…15分．
（向量写出，夹角公式写出，计算答案错误至少给2分）
非向量做法：指出角给（2分），其他视情况相应给分

点评 本题考查直线与平面平行，点线面距离的求法，异面直线所成角的求法，考查会计信息能力，以及计算能力．