【答案】
分析:(1)由已知中圆C过点P(1,1),且圆M:(x+2)
2+(y+2)
2=r
2(r>0)关于直线x+y+2=0对称,我们可以求出圆C的方程,然后判断圆心距CM与两圆半径和与差的关系,即可得到答案.
(2)分直线l的斜率不存在和存在两种情况,根据直线截圆C的弦长等于2,分别求得直线l的方程.
(3)由已知中直线PA和直线PB与x轴分别交于点G、H,且∠PGH=∠PHG,可得直线PA和直线PB的斜率存在,且互为相反数,设PA:y-1=k(x-1),PB:y-1=-k(x-1),求出A,B坐标后,代入斜率公式,判断直线OP和AB是否相等,即可得到答案.
解答:解:(1)由题意可得点C和点M(-2,-2)关于直线x+y+2=0对称,且圆C和圆M的半径相等,都等于r.
设C(m,n),由

•(-1)=-1,且

求得

,
故原C的方程为 x
2+y
2=r
2.
再把点P(1,1)代入圆C的方程,求得r=

,故圆的方程为 x
2+y
2=2.
(2)直线l过点Q(1,0.5),当直线l的斜率不存在时,方程为x=1,截圆C得到的弦长等于2

=2,满足条件.
当直线l的斜率存在时,设直线l的方程为y-0.5=k(x-1),即 kx-y+0.5-k=0,则圆心C到直线l的距离d=

,
再由弦长公式可得 2=2

,解得k=-

,故所求的直线方程为-

x-y+

+

=0,即 3x+4y-5=0.
综上可得,直线l的方程为 x=1,或 3x+4y-5=0.
(3)过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,
则得直线OP和AB平行,理由如下:
由题意知,直线PA和直线PB的斜率存在,且互为相反数,故可设PA:y-1=k(x-1),PB:y-1=-k(x-1).
由

,得(1+k
2)x
2+2k(1-k)x+(1-k)
2-2=0,
因为P的横坐标x=1一定是该方程的解,故可得x
A=

.…(12分)
同理,所以x
B=

,由于AB的斜率k
AB=
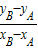
=

=

=1=k
OP (OP的斜率),(15分)
所以,直线AB和OP一定平行.
点评:本题考查的知识点是直线和圆的方程的应用,点到直线的距离公式,关于直线对称的圆的方程,圆与圆位置关系及其判定,其中根据已知条件求出圆C的方程是解答本题的关键,体现了分类讨论的数学思想,属于中档题.

 •(-1)=-1,且
•(-1)=-1,且  求得
求得  ,
, ,故圆的方程为 x2+y2=2.
,故圆的方程为 x2+y2=2. =2,满足条件.
=2,满足条件. ,
, ,解得k=-
,解得k=- ,故所求的直线方程为-
,故所求的直线方程为- x-y+
x-y+ +
+ =0,即 3x+4y-5=0.
=0,即 3x+4y-5=0. ,得(1+k2)x2+2k(1-k)x+(1-k)2-2=0,
,得(1+k2)x2+2k(1-k)x+(1-k)2-2=0, .…(12分)
.…(12分) ,由于AB的斜率kAB=
,由于AB的斜率kAB=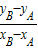 =
= =
= =1=kOP (OP的斜率),(15分)
=1=kOP (OP的斜率),(15分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案