
分析 利用余弦定理与三角形的面积公式,化简$\frac{AC}{AB}$+$\frac{AB}{AC}$+$\frac{B{C}^{2}}{AB•AC}$为C的三角函数,通过两角和化简函数为一个角的一个三角函数的形式,求出表达式的最大值.
解答 解:在△ABC中,AB=c,AC=b,BC=a,
所以 $\frac{AC}{AB}$+$\frac{AB}{AC}$+$\frac{B{C}^{2}}{AB•AC}$=$\frac{{c}^{2}+{b}^{2}-{a}^{2}}{bc}$,
因为a2=c2+b2-2bccosA,
所以:$\frac{{c}^{2}+{b}^{2}-{a}^{2}}{bc}$=$\frac{2{a}^{2}+2bccosA}{bc}$,
△ABC中,BC边上的高与BC边的长相等,
所以:$\frac{1}{2}$bcsinA=$\frac{1}{2}$a2,
即bcsinA=a2,
∴$\frac{2{a}^{2}+2bccosA}{bc}$=$\frac{2bcsinA+2bccosA}{bc}$=2sinA+2cosA
=2$\sqrt{2}$sin(C+$\frac{π}{4}$)≤2$\sqrt{2}$.
则$\frac{AC}{AB}$+$\frac{AB}{AC}$+$\frac{B{C}^{2}}{AB•AC}$的最大值为:2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查余弦定理与三角形的面积公式的应用,两角和的正弦函数的应用,考查计算能力,属于中档题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源:2017届河北沧州市高三9月联考数学(文)试卷(解析版) 题型:选择题
将函数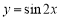 的图像向左平移
的图像向左平移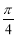 个单位,所得函数图像的一条对称轴方程为( )
个单位,所得函数图像的一条对称轴方程为( )
A.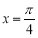 B.
B.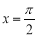 C.
C.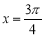 D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
函数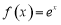 ,
,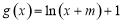 ,(
,(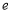 是自然对数的底数,
是自然对数的底数,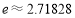 ).
).
(Ⅰ)求函数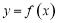 的图象在点
的图象在点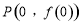 的切线
的切线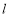 的方程;
的方程;
(Ⅱ)若对任意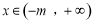 ,恒有
,恒有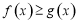 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-2,1) | C. | (-1,1) | D. | (-1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com