
分析 由题意可知,bn就相当于San,利用前n项和与通项an的关系式:Sn-Sn-1=an(n≥2),S1=a1(n=1),求解
解答 解:由题意可知,bn就相当于San;
∵Sn-Sn-1=an(n≥2),S1=a1(n=1),可得:[(2n-1)3n+4]-[(2n-2-1)3n-1+4]=an(n≥2)
解得:${a}_{n}=4n•{3}^{n-1}$(n≥2)
当n=1时,b1=a1=7
故答案为:${a_n}=\left\{\begin{array}{l}7(n=1)\\ 4n•{3^{n-1}}(n≥2)\end{array}\right.$
点评 本题考查了数列的通项an与前n项和Sn的关系式:Sn-Sn-1=an(n≥2),S1=a1(n=1)的运用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(文)试卷(解析版) 题型:选择题
设函数 ,若对任意
,若对任意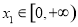 ,都存在
,都存在 ,使得
,使得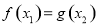 ,则实数
,则实数 的最大值为( )
的最大值为( )
A.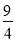 B.2 C.
B.2 C. D.4
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 等腰非直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com