
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 将运动员按成绩由好到差分为6组,成绩在[130,151]内的恰好有5组,从而得到用系统抽样方法从中抽取6人,其中成绩在区间[130,151]上的运动员人数是5人.
解答 解:将运动员按成绩由好到差分为6组,
则第一组(130,130,133,134,135),
第二组(136,136,138,138,138),
第三组(141,141,141,142,142),
第四组(142,143,143,144,144),
第五组(145,145,145,150,151),
第六组(152,152,153,153,153),
故成绩在[130,151]内的恰好有5组,
∴用系统抽样方法从中抽取6人,则其中成绩在区间[130,151]上的运动员人数是5人.
故选:C.
点评 本题考查抽取的人数的求法,是基础题,解题时要认真审题,注意系统抽样的性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(理)试卷(解析版) 题型:解答题
已知函数 .
.
(1)求函数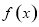 的单调区间和极值;
的单调区间和极值;
(2)证明:当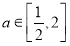 时,函数
时,函数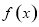 没有零点(提示:
没有零点(提示: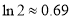 ).
).
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(文)试卷(解析版) 题型:选择题
将函数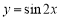 的图像向左平移
的图像向左平移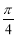 个单位,所得函数图像的一条对称轴方程为( )
个单位,所得函数图像的一条对称轴方程为( )
A.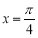 B.
B.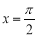 C.
C.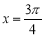 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P=$\frac{S}{M}$ | B. | P>$\frac{S}{M}$ | C. | P2=($\frac{S}{M}$)n | D. | P2>($\frac{S}{M}$)n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-2,1) | C. | (-1,1) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},\frac{11}{2})$ | B. | $(\frac{1}{2},\frac{1}{2})$ | C. | $(\frac{5}{2},\frac{7}{2})$ | D. | $(\frac{3}{2},\frac{7}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com