
设二次函数 ,对任意实数
,对任意实数 ,有
,有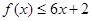 恒成立;数列
恒成立;数列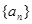 满足
满足 .
.
(1)求函数 的解析式和值域;
的解析式和值域;
(2)试写出一个区间 ,使得当
,使得当 时,数列
时,数列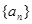 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)已知 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有

 恒成立,若存在,
恒成立,若存在,
求之;若不存在,说明理由.
解:(1)由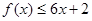 恒成立等价于
恒成立等价于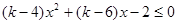 恒成立,…1分
恒成立,…1分
从而得: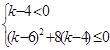 ,化简得
,化简得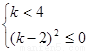 ,从而得
,从而得 ,
,
所以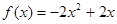 ,………3分
,………3分
其值域为 .…………………4分
.…………………4分
(2)解:当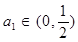 时,数列
时,数列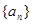 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下:
设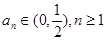 ,则
,则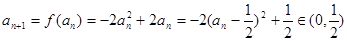 ,
,
所以对一切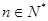 ,均有
,均有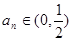 ;………………7分
;………………7分
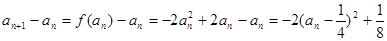
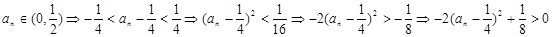
从而得 ,即
,即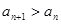 ,所以数列
,所以数列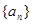 在区间
在区间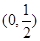 上是递增数列…10分
上是递增数列…10分
注:本题的区间也可以是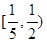 、
、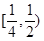 、
、 等无穷多个.
等无穷多个.
另解:若数列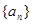 在某个区间上是递增数列,则
在某个区间上是递增数列,则
即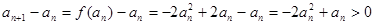
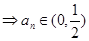 …7分
…7分
又当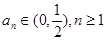 时,
时,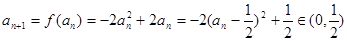 ,
,
∴对一切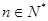 ,均有
,均有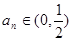 且
且 ,
,
∴数列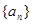 在区间
在区间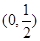 上是递增数列.…………………………10分
上是递增数列.…………………………10分
(3)(文科)由(2)知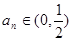 ,从而
,从而 ;
;
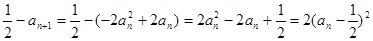 ,
,
即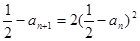 ; ………12分
; ………12分
令 ,则有
,则有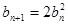 且
且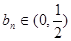 ;
;
从而有 ,可得
,可得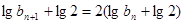 ,
,
∴数列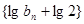 是以
是以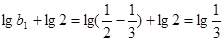 为首项,公比为
为首项,公比为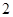 的等比数列,………14分
的等比数列,………14分
从而得 ,即
,即 ,
,
∴ 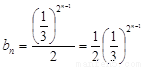 ,
,
∴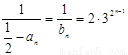 ,∴
,∴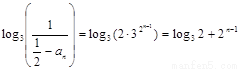 , …16分
, …16分
∴,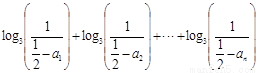
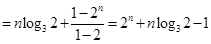 .
………………………18分
.
………………………18分
(3)(理科)由(2)知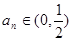 ,从而
,从而 ;
;
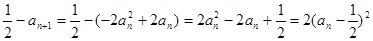 ,
,
即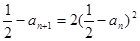 ;………12分
;………12分
令 ,则有
,则有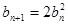 且
且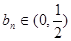 ;
;
从而有 ,可得
,可得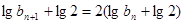 ,所以数列
,所以数列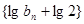 是
是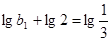 为首项,公比为
为首项,公比为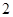 的等比数列,…………………14分
的等比数列,…………………14分
从而得 ,即
,即 ,
,
所以 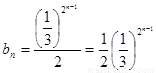 ,
,
所以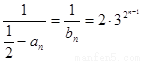 ,所以
,所以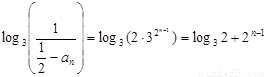 ,
,
所以,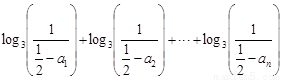
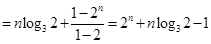 .………………………16分
.………………………16分
即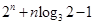
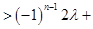
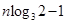 ,所以,
,所以,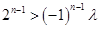 恒成立
恒成立
(1)当n为奇数时,即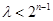 恒成立,当且仅当
恒成立,当且仅当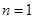 时,
时,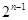 有最小值
有最小值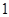 为。
为。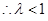
(2)当n为偶数时,即 恒成立,当且仅当
恒成立,当且仅当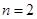 时,有最大值
时,有最大值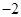 为。
为。
所以,对任意 ,有
,有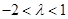 。又
。又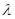 非零整数,
非零整数,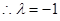 …………18分
…………18分
【解析】略


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源:2011年辽宁省沈阳二中高二上学期10月月考数学 题型:解答题
(本题满分12分)
设二次函数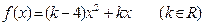 ,对任意实数
,对任意实数 ,有
,有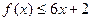 恒成立;数列
恒成立;数列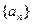 满足
满足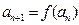 .
.
(1)求函数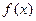 的解析式;
的解析式;
(2)试写出一个区间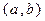 ,使得当
,使得当 时,
时,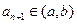 且数列
且数列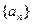 是递增数列,并说明理由;
是递增数列,并说明理由;
(3)已知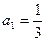 ,是否存在非零整数
,是否存在非零整数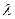 ,使得对任意
,使得对任意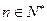 ,都有
,都有
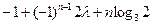 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海市长宁区高三上学期教学质量检测文科数学试卷(解析版) 题型:解答题
设二次函数 ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
.
(1)求函数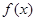 的解析式和值域;
的解析式和值域;
(2)证明:当 时,数列
时,数列 在该区间上是递增数列;
在该区间上是递增数列;
(3)已知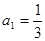 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有

 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省高三第一次月考文科数学试卷(解析版) 题型:解答题
设二次函数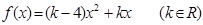 ,对任意实数
,对任意实数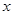 ,
,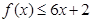 恒成立;正数数列
恒成立;正数数列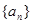 满足
满足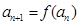 .
.
(1)求函数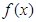 的解析式和值域;
的解析式和值域;
(2)试写出一个区间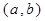 ,使得当
,使得当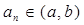 时,数列
时,数列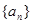 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)若已知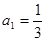 ,求证:数列
,求证:数列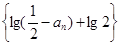 是等比数列
是等比数列
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市静安区高三下学期质量调研考试数学理卷 题型:选择题
.(本题满分18分)
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设二次函数 ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
.
(1)求函数 的解析式和值域;
的解析式和值域;
(2)试写出一个区间 ,使得当
,使得当 时,数列
时,数列 在这个区间上是递增数列,
在这个区间上是递增数列,
并说明理由;
(3)已知 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有

 恒成立,若存在,
恒成立,若存在,
求之;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com