
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<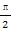 )的部分图象如图所示.
)的部分图象如图所示.
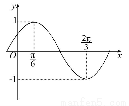
(1)求f(x)的最小正周期及解析式.
(2)设g(x)=f(x)-cos2x,求函数g(x)在区间[0,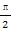 ]上的最大值和最小值.
]上的最大值和最小值.
(1) f(x)=sin(2x+ )
)
(2) 当2x- =
= ,即x=
,即x= 时,g(x)取最大值为1;
时,g(x)取最大值为1;
当2x- =-
=- ,即x=0时,g(x)取最小值为-
,即x=0时,g(x)取最小值为-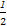 .
.
【解析】【思路点拨】(1)由图象及题设中的限制条件可求A,ω,φ.
(2)将f(x)代入g(x)整理化简为一个三角函数,再由x的范围求最值即可.
【解析】
(1)由图可得A=1,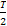 =
=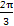 -
- =
= ,所以T=π,所以ω=2.
,所以T=π,所以ω=2.
当x= 时,f(x)=1,
时,f(x)=1,
可得sin(2× +φ)=1,
+φ)=1,
因为|φ|< ,所以φ=
,所以φ= .
.
所以f(x)的解析式为f(x)=sin(2x+ ).
).
(2)g(x)=f(x)-cos2x
=sin(2x+ )-cos2x
)-cos2x
=sin2xcos +cos2xsin
+cos2xsin -cos2x
-cos2x
= sin2x-
sin2x-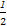 cos2x
cos2x
=sin(2x- ).
).
因为0≤x≤ ,所以-
,所以- ≤2x-
≤2x- ≤
≤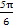 .
.
当2x- =
= ,即x=
,即x= 时,g(x)取最大值为1;
时,g(x)取最大值为1;
当2x- =-
=- ,即x=0时,g(x)取最小值为-
,即x=0时,g(x)取最小值为-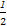 .
.
【方法技巧】由图象求解析式和性质的方法和技巧
(1)给出图象求y=Asin(ωx+φ)+b的解析式的难点在于ω,φ的确定,本质为待定系数,基本方法是①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到,通常可由平衡点或最值点确定周期T,进而确定ω.
(2)由图象求性质的时候,首先确定解析式,再根据解析式求其性质,要紧扣基本三角函数的性质.例如,单调性、奇偶性、周期性和对称性等都是考查的重点和热点.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心,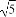 为半径的圆的方程为( )
为半径的圆的方程为( )
(A)x2+y2-2x+4y=0 (B)x2+y2+2x+4y=0
(C)x2+y2+2x-4y=0 (D)x2+y2-2x-4y=0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷(解析版) 题型:填空题
坐标平面上有两个定点A,B和动点P,如果直线PA,PB的斜率之积为定值m,则点P的轨迹可能是:①椭圆;②双曲线;③抛物线;④圆;⑤直线.试将正确的序号填在横线上: .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
若点A(3,5)关于直线l:y=kx的对称点在x轴上,则k是( )
(A) (B)±
(B)±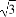
(C)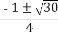 (D)
(D)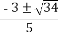
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
平面直角坐标系中直线y=2x+1关于点(1,1)对称的直线方程是( )
(A)y=2x-1 (B)y=-2x+1
(C)y=-2x+3 (D)y=2x-3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十第三章第四节练习卷(解析版) 题型:选择题
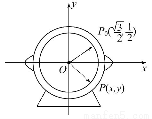
如图,为了研究钟表与三角函数的关系,建立了如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0(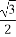 ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
(A)y=sin(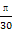 t+
t+ ) (B)y=sin(-
) (B)y=sin(-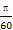 t-
t- )
)
(C)y=sin(-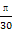 t+
t+ ) (D)y=sin(-
) (D)y=sin(-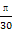 t-
t-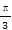 )
)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十四第三章第八节练习卷(解析版) 题型:解答题
在海岸A处,发现北偏东45°方向、距离A处(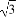 -1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10
-1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10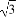 海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十六第四章第二节练习卷(解析版) 题型:填空题
已知向量a=(-2,3),b∥a,向量b的起点为A(1,2),终点B在坐标轴上,则点B的坐标为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十五第四章第一节练习卷(解析版) 题型:选择题
在以下各命题中,假命题的个数为( )
①“|a|=|b|”是“a=b”的必要不充分条件
②任一非零向量的方向都是唯一的
③“a∥b”是“a=b”的充分不必要条件
④若|a|-|b|=|a|+|b|,则b=0
(A)1(B)2(C)3(D)4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com