
【题目】设抛物线的顶点在坐标原点,焦点![]() 在
在![]() 轴上,过点
轴上,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,线段
两点,线段![]() 的长度为8,
的长度为8, ![]() 的中点到
的中点到![]() 轴的距离为3.
轴的距离为3.
(1)求抛物线的标准方程;
(2)设直线![]() 在
在![]() 轴上的截距为6,且抛物线交于
轴上的截距为6,且抛物线交于![]() 两点,连结
两点,连结![]() 并延长交抛物线的准线于点
并延长交抛物线的准线于点![]() ,当直线
,当直线![]() 恰与抛物线相切时,求直线
恰与抛物线相切时,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
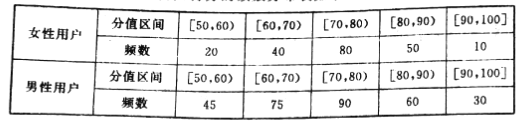
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示2×2方格,在每一个方格中填入一个数字,数字可以是1、2、3、4中的任何一个,允许重复.若填入A方格的数字大于B方格的数字,则不同的填法共有( )
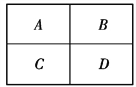
A. 192种 B. 128种 C. 96种 D. 12种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
A小区 | 低碳族 | 非低碳族 |
比例 |
|
|
B小区 | 低碳族 | 非低碳族 |
比例 |
|
|
C小区 | 低碳族 | 非低碳族 |
比例 |
|
|
(1)从A,B,C三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为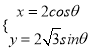 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,与直角坐标系
轴的正半轴为极轴,与直角坐标系![]() 取相同的单位长度建立极坐标系,曲线
取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)化曲线![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线![]() 与
与![]() 轴的一个交点的坐标为
轴的一个交点的坐标为![]() ,经过点
,经过点![]() 作斜率为1的直线,
作斜率为1的直线, ![]() 交曲线
交曲线![]() 于
于![]() 两点,求线段
两点,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数),现随机抽取20天的指数(见下表),将指数不低于![]() 视为当天空气质量优良.
视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
(1)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(2)以这20天的数据估计我市总体空气质量(天数很多),若从我市总体空气质量指数中随机抽取3天的指数,用![]() 表示抽到空气质量为优良的天数,求
表示抽到空气质量为优良的天数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com