【题目】某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，记其质量指标值为
，当
时，产品为一级品；当
时，产品为二级品；当
时，产品为三级品.现用两种新配方（分别称为
配方和
配方）做实验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：
配方的频数分布表
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 5 | 10 | 15 | 30 | 40 |
（1）从配方生产的产品中按等级分层抽样抽取5件产品，再从这5件产品中任取3件，求恰好取到1件二级品的频率；
（2）若这种新产品的利润率
与质量指标满足如下条件：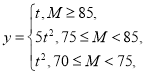
，其中
，请分别计算两种配方生产的产品的平均利润率，如果从长期来看，你认为投资哪种配方的产品平均利润率较大?
【答案】（1）
（2）
配方生产的产品平均利润率为
，
配方生产的产品平均利润率为
，投资配方的产品平均利润率较大
【解析】
（1）按分层抽样抽取的5件产品中有2件为二级品，记为
，
，有3件为一级品，记为
，
，
，可得从这5件产品中任取3件的取法及恰好取到1件的取法，可得答案；
（2）分别将
与
用
表示，计算出
的值，由
可得哪种配方的产品平均利润率较大.
解：（1）由题知，按分层抽样抽取的5件产品中有2件为二级品，记为，，有3件为一级品，记为，，，
从5件产品中任取3件共有10种取法，枚举如下：
，
，
，
，
，
，
，
，
，
其中恰好取到1件二级品共有6种取法，所以恰好取到1件二级品的概率为
.
（2）由题知配方生产的产品平均利润率
，
配方生产的产品平均利润率
，
所以
，
因为
，所以
，所以投资配方的产品平均利润率较大.
科目：高中数学 来源： 题型：
【题目】给定椭圆C:
(
),称圆心在原点O,半径为
的圆是椭圆C的“卫星圆”.若椭圆C的离心率
,点
在C上.
(1)求椭圆C的方程和其“卫星圆”方程;
(2)点P是椭圆C的“卫星圆”上的一个动点,过点P作直线
,
使得
,与椭圆C都只有一个交点,且,分别交其“卫星圆”于点M,N,证明:弦长
为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某书店今年5月上架10种新书，且它们的首月销量（单位：册）情况为：100，50，100，150，150，100，150，50，100，100，频率为概率，解答以下问题：
（1）若该书店打算6月上架某种新书，估计它首月销量至少为100册的概率；
（2）若某种最新出版的图书订购价为10元/册，该书店计划首月内按12元/册出售，第二个月起按8元/册降价出售，降价后全部存货可以售出.试确定，该书店订购该图书50册，100册，还是150册有利于获得更多利润？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，
是抛物线
的焦点，过点且与坐标轴不垂直的直线交抛物线于
、
两点，交抛物线的准线于点
，其中
，
．过点作
轴的垂线交抛物线于点
，直线
交抛物线于点
.
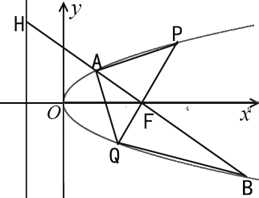
（1）求
的值；
（2）求四边形
的面积
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知三棱柱
中，
底面
，
，
，
，
.
，
分别为棱
，
的中点.
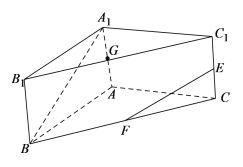
（1）求异面直线
与
所成角的大小；
（2）若
为线段
的中点，试在图中作出过、、三点的平面截该棱柱所得的多边形，并求出以该多边形为底，
为顶点的棱锥的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
