练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中，O是平面ABC上的一点，动点P满足
    OP
    =
    OA
    +λ(
    OB
    +
    OC
    )    ，λ∈R，则点P的轨迹过△ABC的（　　）
    分析：根据向量的加法的平行四边形法则向量的运算法则，对
    OP
    =
    OA
    +λ(
    OB
    +
    OC
    )    进行化简，得到
    OP
    =
    OA
    +λ(
    OB
    +
    OC
    )    ，根据三点共线的充要条件知道P、A、D三点共线，从而得到点P的轨迹一定经过△ABC的重心．
    解答：解：取BC的中点D，则 2
    OD
    =
    OC
    +
    OB

    ∵
    OP
    =
    OA
    +λ(
    OB
    +
    OC
    )
    ∴
    OP
    =
    OA
    +2λ
    OD

    ∴P、A、D三点共线，
    ∴点P的轨迹一定经过△ABC的重心．
    故选B．
    点评：此题是个中档题．考查向量的加法法则和运算法则，以及三点共线的充要条件，和三角形的五心问题，综合性强，体现了数形结合的思想．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    点O在△ABC所在平面上，若
    OA
    •
    OB
    =
    OB
    •
    OC
    =
    OC
    •
    OA
    ，则点O是△ABC的（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•渭南三模）平面上：在正三角形ABC中，若D是BC的中点，G是三角形ABC的重心，则
    AG
    GD
    =2    ；空间中：在正四面体ABCD中，若三角形BCD中心为M，正四面体ABCD中心为O，则
    AO
    OM
    =
    3
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源：2014届四川省攀枝花市高二上学期期中理科数学试卷（解析版） 题型：填空题

    下列命题：①若与共线，则存在唯一的实数，使=；

    ②空间中，向量、、共面，则它们所在直线也共面；

    ③P是△ABC所在平面外一点，O是点P在平面上的射影．若PA 、PB、PC两两垂直，则O是△ABC垂心．

    ④若三点不共线，是平面外一点．,则点一定在平面上，且在△ABC内部，上述命题中正确的命题是                   ．

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年黑龙江省哈尔滨六中高一（上）期末数学试卷（解析版） 题型：选择题

    点O在△ABC所在平面上，若，则点O是△ABC的（ ）
    A．三条中线交点
    B．三条高线交点
    C．三条边的中垂线交点
    D．三条角分线交点

    查看答案和解析>>

    科目：高中数学 来源：2011年陕西省渭南市高考数学三模试卷（理科）（解析版） 题型：解答题

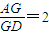    平面上：在正三角形ABC中，若D是BC的中点，G是三角形ABC的重心，则；空间中：在正四面体ABCD中，若三角形BCD中心为M，正四面体ABCD中心为O，则=    ．

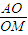    查看答案和解析>>

    同步练习册答案