
【题目】已知函数![]() 函数在点
函数在点![]() 处的切线为
处的切线为![]() .
.
(1)求函数![]() 的值,并求出
的值,并求出![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)若![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() 时,
时,![]() 为增函数,
为增函数,![]() 时,
时,![]() 为减函数;(2)证明见解析.
为减函数;(2)证明见解析.
【解析】
试题分析:(1)先利用切点和斜率,列方程组,求得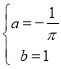 ,此时
,此时![]() ,将区间分为
,将区间分为![]() 和
和![]() 来研究函数的单调性,其中
来研究函数的单调性,其中![]() 部分要用二阶导数来求;(2)根据
部分要用二阶导数来求;(2)根据![]() ,代入函数的表达式,化简得
,代入函数的表达式,化简得![]() ,令
,令![]() ,换元后构造函数
,换元后构造函数![]() ,利用导数证明,
,利用导数证明,![]() .
.
试题解析:
(1)由题意:![]() ,所以
,所以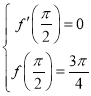 ,解得
,解得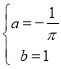 ,
,
故![]() ..................2分
..................2分
当![]() 时,
时,![]() 为减函数,且
为减函数,且![]() 为增函数,.................3分
为增函数,.................3分
当![]() 时,
时,![]() 为增函数,且
为增函数,且![]() ,
,
故存在唯一![]() 使
使![]() ,所以
,所以![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
又因为![]() ,所以
,所以![]() 时,
时,![]() 为减函数,............5分
为减函数,............5分
综上可知:![]() 时,
时,![]() 为增函数;
为增函数;
![]() 时,
时,![]() 为减函数.........................6分
为减函数.........................6分
(2)由![]() ,得
,得![]() ,
,
所以![]() ,两边同除以
,两边同除以![]() ,
,
得![]() ,令
,令![]() ,则
,则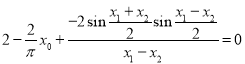 ,
,
所以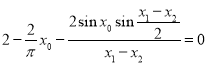 ,得
,得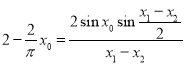 ......8分
......8分
因为![]() ,所以
,所以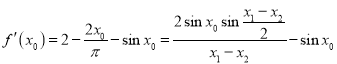
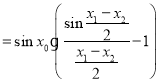 .............................9分
.............................9分
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 为减函数,
为减函数,
当![]() 时,
时,![]() 为减函数,........................11分
为减函数,........................11分
所以![]() ,(也可以利用斜率),所以
,(也可以利用斜率),所以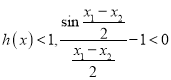 ,
,
又![]() ,所以
,所以![]() ,故
,故![]() ,........................12分
,........................12分


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数比女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(Ⅰ)根据题意建立的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
(Ⅱ)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
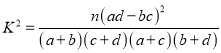 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 、
、![]() 为常数).
为常数).
(Ⅰ)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当函数![]() 在
在![]() 处取得极值
处取得极值![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(Ⅲ)当![]() 时,设
时,设![]() ,若函数
,若函数![]() 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距32海里的
处,此时测得其东北方向与它相距32海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处.
海里处.

(1)求此时该外国船只与![]() 岛的距离;
岛的距离;
(2)观测中发现,此外国船只正以每小时8海里的速度沿正南方向航行,为了将该船拦截在离![]() 岛24海里处,不让其进入
岛24海里处,不让其进入![]() 岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对绵阳南山实验学校的500名教师的年龄进行统计分析,年龄的频率分布直方图如图所示,规定年龄在![]() 内的为青年教师,
内的为青年教师,![]() 内的为中年教师,
内的为中年教师,![]() 内的为老年教师.
内的为老年教师.
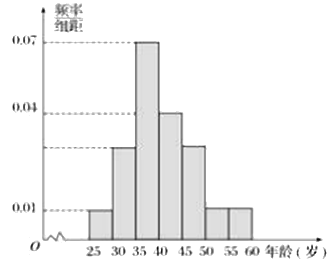
(1)求年龄![]() ,
,![]() 内的教师人数;
内的教师人数;
(2)现用分层抽样的方法从中、青年中抽取18人进行同课异构课堂展示,求抽到年龄在![]() 内的人数.
内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,小波从![]() 街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是
街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是![]() ,红灯亮的概率都是
,红灯亮的概率都是![]() .
.
(1)求小波遇到4次绿灯后,处于![]() 街区的概率;
街区的概率;
(2)若小波一共遇到了3次红绿灯,设此时小波所处的街区与![]() 街区相距的街道数为
街区相距的街道数为![]() (如小波若处在
(如小波若处在![]() 街区则相距零个街道,处在
街区则相距零个街道,处在![]() ,
,![]() 街区都是相距2个街道),求
街区都是相距2个街道),求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com