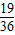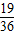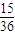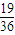Question

两个骰子的点数分别为b，c，则方程x²+bx+c=0有两个实根（包括相等）的概率等于    ．

Answer 1

【答案】分析：根据已知中两个骰子的点数分别为b，c，我们可以求出所有基本事件的总数，求出满足条件方程x²+bx+c=0有两个实根（包括相等）的基本事件个数后，代入古典概型公式，即可得到答案．
解答：解：两个骰子的点数分别为b，c，共有：
（1，1），（1，2），（1，3），（1，4），（1，5），（1，6）
（2，1），（2，2），（2，3），（2，4），（2，5），（2，6）
（3，1），（3，2），（3，3），（3，4），（3，5），（3，6）
（4，1），（4，2），（4，3），（4，4），（4，5），（4，6）
（5，1），（5，2），（5，3），（5，4），（5，5），（5，6）
（6，1），（6，2），（6，3），（6，4），（6，5），（6，6）共36中情况
若方程x²+bx+c=0有两个实根（包括相等）则b²-4c≥0，
满足条件的基本情况有：
（2，1），（3，1），（3，2），（4，1），（4，2），（4，3），
（4，4），（5，1），（5，2），（5，3），（5，4），（5，5），
（5，6），（6，1），（6，2），（6，3），（6，4），（6，5），（6，6）共19中情况
故方程x²+bx+c=0有两个实根（包括相等）的概率P=
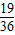
故答案为：
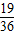点评：本题考查的知识点是古典概型及其概率计算公式，列举法计算基本事件数及事件发生的概率，其中计算出基本事件总数及满足条件的基本事件个数是解答本题的关键．