
分析 (Ⅰ)设点D的坐标为(x,y),求出A1、A2的坐标,由题意和斜率公式列出方程化简,可得点D的轨迹C2的方程;
(Ⅱ)设P(x1,y1),Q(x2,y2),联立直线方程和C2的方程消去y,由条件可得△=0并化简,联立直线l与圆C1的方程消去x,利用韦达定理写出表达式,由图象和三角形的面积公式表示出${S}_{△PO{A}_{1}}{+S}_{△PO{A}_{2}}$,化简后利用基本不等式求出△POA1与△QOA2的面积之和的最大值.
解答  解:(Ⅰ)设点D的坐标为(x,y),
解:(Ⅰ)设点D的坐标为(x,y),
∵圆C1:x2+y2=4与x轴左右交点分别为点A1(-2,0),A2(2,0),
且l1与l2斜率的乘积为-$\frac{1}{4}$,
∴$\frac{y}{x+2}•\frac{y}{x-2}=-\frac{1}{4}$,化简得$\frac{{x}^{2}}{4}+{y}^{2}=1(x≠±2)$,
∴点D的轨迹C2方程是$\frac{{x}^{2}}{4}+{y}^{2}=1(x≠±2)$;
(Ⅱ)设P(x1,y1),Q(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得,(1+4k2)x2+8kmx+4m2-4=0,
由题意得,△=64k2+16-16m2=0,
化简得,m2=4k2+1,
联立$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$消去x得,(1+k2)y2-2my+1=0,
∴△=4m2-4(1+k2)=12k2>0,
y1+y2=$\frac{2m}{1+{k}^{2}}$,${y}_{1}{y}_{2}=\frac{1}{1+{k}^{2}}$>0,则y1,y2同号,
由r=2得,${S}_{△PO{A}_{1}}$+${S}_{△PO{A}_{2}}$=$\frac{1}{2}r|{y}_{1}|$+$\frac{1}{2}r|{y}_{2}|$=$\frac{1}{2}r|{y}_{1}+{y}_{2}|$
=$\frac{2|m|}{1+{k}^{2}}$=$\frac{2\sqrt{1+4{k}^{2}}}{1+{k}^{2}}$=$\frac{1}{\sqrt{3}}•$$\frac{2\sqrt{3(1+4{k}^{2})}}{1+{k}^{2}}$≤$\frac{1}{\sqrt{3}}•\frac{3+(1+4{k}^{2})}{1+{k}^{2}}$=$\frac{4}{\sqrt{3}}$,
当且仅当3=1+4k2,即k=$±\frac{\sqrt{2}}{2}$时取等号,
∴${S}_{△PO{A}_{1}}{+S}_{△PO{A}_{2}}$的最大值是$\frac{4\sqrt{3}}{3}$.
点评 本题考查点的轨迹方程的求法,直线与圆、椭圆的位置关系,韦达定理,以及基本不等式求最值的应用,考查化简、变形能力,设而不求数学思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,+∞) | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-2)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
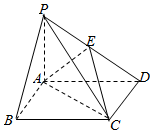 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5+lg7-π | B. | lg7-1+π | C. | 6-π | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com