
【题目】记U={1,2,…,100},对数列{an}(n∈N*)和U的子集T,若T=,定义ST=0;若T={t1 , t2 , …,tk},定义ST= ![]() +
+ ![]() +…+
+…+ ![]() .例如:T={1,3,66}时,ST=a1+a3+a66 . 现设{an}(n∈N*)是公比为3的等比数列,且当T={2,4}时,ST=30.
.例如:T={1,3,66}时,ST=a1+a3+a66 . 现设{an}(n∈N*)是公比为3的等比数列,且当T={2,4}时,ST=30.
(1)求数列{an}的通项公式;
(2)对任意正整数k(1≤k≤100),若T{1,2,…,k},求证:ST<ak+1;
(3)设CU,DU,SC≥SD , 求证:SC+SC∩D≥2SD .
【答案】
(1)解:当T={2,4}时,ST=a2+a4=a2+9a2=30,
因此a2=3,从而a1= ![]() =1,
=1,
故an=3n﹣1
(2)解:ST≤a1+a2+…ak=1+3+32+…+3k﹣1= ![]() <3k=ak+1
<3k=ak+1
(3)解:设A=C(C∩D),B=D(C∩D),则A∩B=,
分析可得SC=SA+SC∩D,SD=SB+SC∩D,则SC+SC∩D﹣2SD=SA﹣2SB,
因此原命题的等价于证明SC≥2SB,
由条件SC≥SD,可得SA≥SB,
①、若B=,则SB=0,故SA≥2SB,
②、若B≠,由SA≥SB可得A≠,设A中最大元素为l,B中最大元素为m,
若m≥l+1,则其与SA<ai+1≤am≤SB相矛盾,
因为A∩B=,所以l≠m,则l≥m+1,
SB≤a1+a2+…am=1+3+32+…+3m﹣1= ![]() ≤
≤ ![]() =
= ![]() ,即SA≥2SB,
,即SA≥2SB,
综上所述,SA≥2SB,
故SC+SC∩D≥2SD
【解析】(1)根据题意,由ST的定义,分析可得ST=a2+a4=a2+9a2=30,计算可得a2=3,进而可得a1的值,由等比数列通项公式即可得答案;(2)根据题意,由ST的定义,分析可得ST≤a1+a2+…ak=1+3+32+…+3k﹣1 , 由等比数列的前n项和公式计算可得证明;(3)设A=C(C∩D),B=D(C∩D),则A∩B=,进而分析可以将原命题转化为证明SC≥2SB , 分2种情况进行讨论:①、若B=,②、若B≠,可以证明得到SA≥2SB , 即可得证明.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某区选派7名队员代表本区参加全市青少年围棋锦标赛,其中3名来自A学校且1名为女棋手,另外4名来自B学校且2名为女棋手.从这7名队员中随机选派4名队员参加第一阶段的比赛.
(1)求在参加第一阶段比赛的队员中,恰有1名女棋手的概率;
(2)设X为选出的4名队员中A、B两校人数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x2017的方差是4,若yi=2xi﹣1(i=1,2,…,2017),则y1 , y2 , …y2017的方差为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程选讲]
在平面直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1 , C2的极坐标方程分别为ρ=2sinθ,ρcos(θ﹣ ![]() )=
)= ![]() .
.
(Ⅰ)求C1和C2交点的极坐标;
(Ⅱ)直线l的参数方程为:  (t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.
(t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系xoy中,曲线C1的参数方程为 ![]() (β为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4cosθ.
(β为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4cosθ.
(Ⅰ)将曲线C1的方程化为极坐标方程;
(Ⅱ)已知直线l的参数方程为 ![]() (
( ![]() <α<π,t为参数,t≠0),l与C1交与点A,l与C2交与点B,且|AB|=
<α<π,t为参数,t≠0),l与C1交与点A,l与C2交与点B,且|AB|= ![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】持续性的雾霾天气严重威胁着人们的身体健康,汽车排放的尾气是造成雾霾天气的重要因素之一.为了贯彻落实国务院关于培育战略性新兴产业和加强节能减排工作的部署和要求,中央财政安排专项资金支持开展私人购买新能源汽车补贴试点.2017年国家又出台了调整新能源汽车推广应用财政补贴的新政策,其中新能源乘用车推广应用补贴标准如表: 某课题组从汽车市场上随机选取了20辆纯电动乘用车,根据其续驶里程R(单词充电后能行驶的最大里程,R∈[100,300])进行如下分组:第1组[100,150),第2组[150,200),第3组[200,250),第4组[250,300],制成如图所示的频率分布直方图.已知第1组与第3组的频率之比为1:4,第2组的频数为7.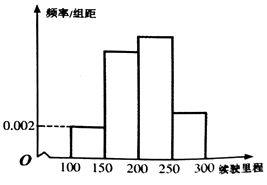
纯电动续驶里程R(公里) | 100≤R<150 | 150≤R<250 | R>250 |
补贴标准(万元/辆) | 2 | 3.6 | 44 |
(1)请根据频率分布直方图统计这20辆纯电动乘用车的平均续驶里程;
(2)若以频率作为概率,设ξ为购买一辆纯电动乘用车获得的补贴,求ξ的分布列和数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC= ![]() CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥CD.
CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥CD. 
(Ⅰ)若E是PC的中点,求证:AP∥平面BDE;
(Ⅱ)求证:平面PCD⊥平面ABCD;
(Ⅲ)求二面角A﹣PB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC= ![]() ,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
(Ⅰ)证明:BE⊥平面ACF;
(Ⅱ)求二面角A﹣BC﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位,所得图象对应的函数( )
个单位,所得图象对应的函数( )
A.在区间[ ![]() ,
, ![]() ]上单调递增
]上单调递增
B.在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
C.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
D.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com