
某种家用电器每台的销售利润与该电器的无故障时间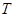 (单位:年)有关,若
(单位:年)有关,若 ,则销售利润为0元;若
,则销售利润为0元;若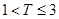 ,则销售利润为100元,若
,则销售利润为100元,若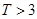 ,则销售利润为200元.设每台该种电器的无故障使用时间
,则销售利润为200元.设每台该种电器的无故障使用时间 ,
,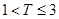 ,
,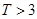 这三种情况发生的概率分别为
这三种情况发生的概率分别为 ,又知
,又知 为方程
为方程 的两根,且
的两根,且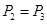 .
.
(1)求 的值;
的值;
(2)记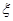 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求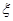 的分布列及数学期望.
的分布列及数学期望.
(Ⅰ)  =
= ,
, =
= ,
,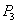 =
= .
.
(Ⅱ)随机变量 的分布列为
的分布列为
|
|
0 |
100 |
200 |
300 |
400 |
|
p |
|
|
|
|
|
所求的数学期望为E =0
=0
 +100
+100
 +200
+200
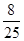 +300
+300
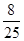 +400
+400
 =240(元)
=240(元)
【解析】
试题分析:(Ⅰ)由已知得 :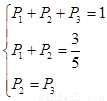
解得: =
= ,
, =
= ,
,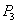 =
= .
.
(Ⅱ) 的可能取值为0,100,200,300,400.
的可能取值为0,100,200,300,400.
P( ="0)="
="0)=" 

 =
= P(
P( ="100)=" 2
="100)=" 2


 =
=
P( ="200)=" 2
="200)=" 2


 +
+

 =
=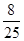 P(
P( ="300)=" 2
="300)=" 2


 =
=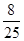
P( ="400)="
="400)=" 

 =
=
随机变量 的分布列为
的分布列为
|
|
0 |
100 |
200 |
300 |
400 |
|
p |
|
|
|
|
|
所求的数学期望为E =0
=0
 +100
+100
 +200
+200
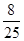 +300
+300
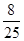 +400
+400
 =240(元)
=240(元)
考点:本题主要考查概率的应用,随机变量的分布列及数学期望。
点评:中档题,近些年的高考题中,概率统计问题,往往以应用题出现。确定随机变量的分布列,关键是计算事件的概率。


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 5 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
某种家用电器每台的销售利润与该电器的无故障使用时间T (单位:年)有关.若T≤1,则销售利润为0元;若1<T≤3,则销售利润为100元;若T>3,则销售利润为200元.设每台该种电器的无故障使用时间T≤1,1<T≤3及T>3这三种情况发生的概率分别为p1,p2,p3,又知p1,p2是方程![]() 的两个根,且p2=p3.
的两个根,且p2=p3.
(1)求p1,p2,p3的值;![]()
(2)记![]() 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
某种家用电器每台的销售利润与该电器的无故障使用时间![]() (单位:年)有关. 若
(单位:年)有关. 若![]() ,则销售利润为
,则销售利润为![]() 元;若
元;若![]() ,则销售利润为
,则销售利润为![]() 元;若
元;若![]() ,则销售利润为
,则销售利润为![]() 元.设每台该种电器的无故障使用时间
元.设每台该种电器的无故障使用时间![]() ,
,![]() 及
及![]() 这三种情况发生的概率分别为
这三种情况发生的概率分别为![]() ,
,![]() ,
,![]() ,叉知
,叉知![]() ,
,![]() 是方程
是方程![]() 的两个根,且
的两个根,且![]() (1)求
(1)求![]() ,
,![]() ,
,![]() 的值; (2)记
的值; (2)记![]() 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求![]() 的期望.
的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com