
在直角坐标平面上,O为原点,M为动点,![]() ,
,![]() .过点M作MM1⊥
.过点M作MM1⊥![]() 轴于M1,过N作NN1⊥
轴于M1,过N作NN1⊥![]() 轴于点N1,
轴于点N1,![]() .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线![]() 交曲线C于两个不同的点P、Q(点Q在A与P之间).
交曲线C于两个不同的点P、Q(点Q在A与P之间).
(Ⅰ)求曲线C的方程;
(Ⅱ)证明不存在直线![]() ,使得
,使得![]() ;
;
(Ⅲ)过点P作![]() 轴的平行线与曲线C的另一交点为S,若
轴的平行线与曲线C的另一交点为S,若![]() ,证明
,证明![]() .
.

(Ⅰ)曲线C的方程:![]() (2)同解析 (3)同解析
(2)同解析 (3)同解析
(1)解:设点T的坐标为![]() ,点M的坐标为
,点M的坐标为![]() ,则M1的坐标为
,则M1的坐标为![]()
![]() ∴点N的坐标为
∴点N的坐标为![]()
∴N1的坐标为![]() ∴
∴![]()
由![]() 有
有 ![]()
∴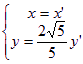 由此得
由此得![]()
由![]() 有
有![]()
∴![]() 即
即![]() ,即为所求的方程.曲线C为椭圆.
,即为所求的方程.曲线C为椭圆.
(2)证:点A(5,0)在曲线C即椭圆的外部,当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 与椭圆C无交点,所以直线
与椭圆C无交点,所以直线![]() 斜率存在,并设为
斜率存在,并设为![]() .直线
.直线![]() 的方程为
的方程为![]() .
.
由方程组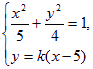 得
得![]()
依题意![]() ,得
,得![]() .
.
当![]() 时,设交点
时,设交点![]() ,PQ的中点为R
,PQ的中点为R![]() ,则
,则
![]() ,
, ![]()
∴![]()
又![]()
![]() BR⊥
BR⊥![]()
![]()
![]()
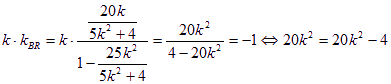
但![]() 不可能成立,所以不存在直线
不可能成立,所以不存在直线![]() 使得
使得![]() .
.
(3)证明:由题有S![]() ,
,![]() .
.
则有方程组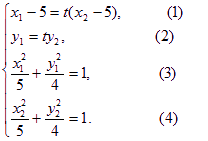
由(1)得:![]()
将(2)、(5)代入(3)有![]()
整理并将(4)、(5)代入得 ![]()
易知![]() ,解得
,解得![]()
因![]() ,故
,故![]() ,
,![]() ,
,
∴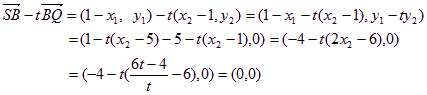
∴![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
| OM |
| 5 |
| ON |
2
| ||
| 5 |
| OM |
| OT |
| M1M |
| N1N |
查看答案和解析>>
科目:高中数学 来源:2010年上海市上海中学高三数学综合练习试卷(4)(解析版) 题型:解答题
 .过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1, .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).查看答案和解析>>
科目:高中数学 来源:2010年广东省高考数学冲刺预测试卷14(文科)(解析版) 题型:解答题
 .过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1, .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).查看答案和解析>>
科目:高中数学 来源:2010年广东省高考数学冲刺预测试卷14(理科)(解析版) 题型:解答题
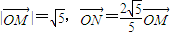 .过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,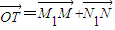 .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com