Question

若函数在区间上单调递减，则实数的取值范围为______.

Answer 1

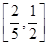
解析试题分析：将函数化成分段函数的形式，不难得到它的减区间为（2，3）．结合题意得：（5a，4a+1）⊆（2，3），由此建立不等关系，解之即可得到实数a的取值范围．解：函数f（x）=|x-2|（x-4）
="(x-2)(x-4)" (x≥2)
(2-x)(x-4) (x＜2)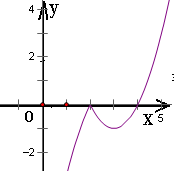

∴函数的增区间为（-∞，2）和（3，+∞），减区间是（2，3）．∵在区间（5a，4a+1）上单调递减，∴（5a，4a+1）⊆（2，3），得2≤5a, 4a+1≤3，解之得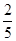≤a≤
故答案为：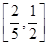
考点：含有绝对值的函数
点评：本题给出含有绝对值的函数，在已知减区间的情况下求参数a的取值范围，着重考查了函数的单调性和单调区间求法等知识，属于中档题