
 与
与 满足:|
满足:| |=4,|
|=4,| |=3,(2
|=3,(2 +3
+3 )•(2
)•(2 -
- )=61.
)=61. •
• 的值;
的值; 与
与 的夹角;
的夹角; -
-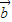 |的值.
|的值. +3
+3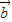 )•(2
)•(2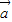 -
-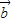 )=61得,4
)=61得,4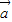 2+4
2+4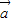 •
•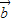 -3
-3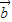 2=61将|
2=61将|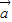 |=4,|
|=4,|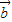 |=3,代入即可求得两向量的内积;
|=3,代入即可求得两向量的内积;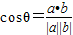 求出向量
求出向量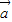 与
与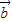 的夹角余弦,再由出对应的角;
的夹角余弦,再由出对应的角;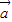 -
-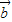 )2=
)2=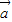 2-2
2-2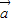 •
•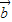 +
+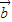 2=13,再开方求出两向量差的模.
2=13,再开方求出两向量差的模.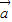 +3
+3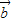 )•(2
)•(2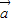 -
-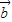 )=61得,4
)=61得,4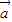 2+4
2+4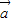 •
•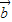 -3
-3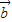 2=61.
2=61.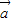 |=4,|
|=4,|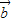 |=3,可得
|=3,可得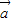 •
•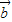 =6. …(4分)
=6. …(4分) 与
与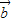 的夹角为θ,
的夹角为θ,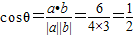 ,
,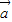 与
与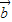 的夹角为60°. …(8分)
的夹角为60°. …(8分)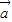 -
-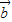 )2=
)2=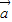 2-2
2-2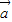 •
•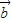 +
+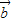 2=13可得,
2=13可得,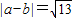 .…(12分)
.…(12分)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com