
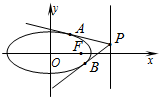
 вбжЊЭждВЕФжааФдкзјБъдЕуЃЌНЙЕудкxжсЩЯЃЌВЂЧвНЙОрЮЊ2ЃЌЖЬжсгыГЄжсЕФБШЪЧ
вбжЊЭждВЕФжааФдкзјБъдЕуЃЌНЙЕудкxжсЩЯЃЌВЂЧвНЙОрЮЊ2ЃЌЖЬжсгыГЄжсЕФБШЪЧ
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
| 3 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| ||
| 2 |
| y0 |
| 3 |
 НтЃКЃЈ1ЃЉЩшЭждВЕФЗНГЬЮЊ
НтЃКЃЈ1ЃЉЩшЭждВЕФЗНГЬЮЊ| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| ||
| 2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| 2 |
| x |
| 4 |
| y |
| 2 |
| x1x |
| 4 |
| y1y |
| 3 |
| x2x |
| 4 |
| y2y |
| 3 |
| y0 |
| 3 |
| y0 |
| 3 |
| y0 |
| 3 |



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
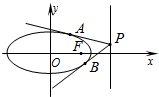
 вбжЊЭждВЕФжааФдкзјБъдЕуOЃЌНЙЕудкxжсЩЯЃЌЖЬжсГЄЮЊ2ЃЌЧвСНИіНЙЕуКЭЖЬжсЕФСНИіЖЫЕуЧЁЮЊвЛИіе§ЗНаЮЕФЖЅЕуЃЎЙ§гвНЙЕуFгыxжсВЛДЙжБЕФжБЯпlНЛЭждВгкPЃЌQСНЕуЃЎ
вбжЊЭждВЕФжааФдкзјБъдЕуOЃЌНЙЕудкxжсЩЯЃЌЖЬжсГЄЮЊ2ЃЌЧвСНИіНЙЕуКЭЖЬжсЕФСНИіЖЫЕуЧЁЮЊвЛИіе§ЗНаЮЕФЖЅЕуЃЎЙ§гвНЙЕуFгыxжсВЛДЙжБЕФжБЯпlНЛЭждВгкPЃЌQСНЕуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
2
| ||
| 5 |
| ||
| 5 |
| AC |
| AO |
| AC |
| AO |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 3 |
| x2 |
| 36 |
| y2 |
| 9 |
| x2 |
| 36 |
| y2 |
| 9 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| ||
| 2 |
| ||
| 2 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com