
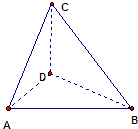
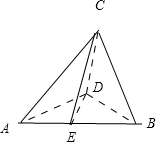
 设Rt△ABC斜边AB上的高是CD,AC=BC=2,沿高CD作折痕将之折成直二面角A-CD-B(如图)那么得到二面角C-AB-D的余弦值等于( )
设Rt△ABC斜边AB上的高是CD,AC=BC=2,沿高CD作折痕将之折成直二面角A-CD-B(如图)那么得到二面角C-AB-D的余弦值等于( )| 2 |
| ||||
| 2 |
| CD2+DE2 |
| 2+1 |
| 3 |
| DE |
| CE |
| 1 | ||
|
| ||
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
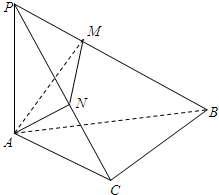 如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,
如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,查看答案和解析>>
科目:高中数学 来源:设计必修五数学苏教版 苏教版 题型:044
如图所示,在Rt△ABC中,∠A、∠B、∠C的对边分别为a、b、c,斜边c是△ABC外接圆的直径(设Rt△ABC外接圆的半径为R),则![]() ,这个结论对钝角三角形、锐角三角形是否也成立呢?你能否结合圆形及初中所学几何知识作出相应的解释?
,这个结论对钝角三角形、锐角三角形是否也成立呢?你能否结合圆形及初中所学几何知识作出相应的解释?

查看答案和解析>>
科目:高中数学 来源:浙江省东阳中学2012届高三上学期期中考试数学理科试题 题型:013
设Rt△ABC的三边分别为a,b,c,其中c为斜边,直线ax+by+c=0与圆cos2![]() ·x2+cos2
·x2+cos2![]() ·y2=1,(
·y2=1,(![]() 为常数,
为常数,![]() ∈(0,
∈(0,![]() )交于M、N两点,则|MN|=
)交于M、N两点,则|MN|=
sin![]()
2sin![]()
tan![]()
2tan![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三上学期期中考试理科数学 题型:选择题
设Rt△ABC的三边分别为a,b,c,其中c为斜边,m]直线ax+by+c=0与圆 ,(
,(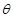 为常数,
为常数,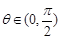 )交于
)交于 两点,则
两点,则
A.sinθ B.2sinθ C.tanθ D.2tanθ
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com