分析:(1)根据三棱柱ABC-A1B1C1是直三棱柱,得到CC1⊥平面ABC,从而AD⊥CC1,结合已知条件AD⊥DE,DE、CC1是平面BCC1B1内的相交直线,得到AD⊥平面BCC1B1,从而平面ADE⊥平面BCC1B1;
(2)先证出等腰三角形△A1B1C1中,A1F⊥B1C1,再用类似(1)的方法,证出A1F⊥平面BCC1B1,结合AD⊥平面BCC1B1,得到A1F∥AD,最后根据线面平行的判定定理,得到直线A1F∥平面ADE.
解答:解:(1)∵三棱柱ABC-A1B1C1是直三棱柱,
∴CC1⊥平面ABC,
∵AD?平面ABC,
∴AD⊥CC1
又∵AD⊥DE,DE、CC1是平面BCC1B1内的相交直线
∴AD⊥平面BCC1B1,
∵AD?平面ADE
∴平面ADE⊥平面BCC1B1;
(2)∵△A1B1C1中,A1B1=A1C1,F为B1C1的中点
∴A1F⊥B1C1,
∵CC1⊥平面A1B1C1,A1F?平面A1B1C1,
∴A1F⊥CC1
又∵B1C1、CC1是平面BCC1B1内的相交直线
∴A1F⊥平面BCC1B1
又∵AD⊥平面BCC1B1,
∴A1F∥AD
∵A1F?平面ADE,AD?平面ADE,
∴直线A1F∥平面ADE.
点评:本题以一个特殊的直三棱柱为载体,考查了直线与平面平行的判定和平面与平面垂直的判定等知识点,属于中档题.

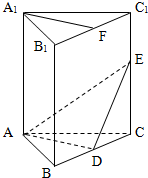 (2012•江苏)如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(2012•江苏)如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:

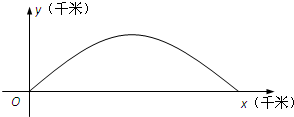 (2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
(2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-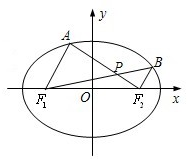 (2012•江苏)如图,在平面直角坐标系xOy中,椭圆
(2012•江苏)如图,在平面直角坐标系xOy中,椭圆