
(本小题12分)
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC—B.

(Ⅰ)试判断直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)求直线BC与平面DEF所成角的余弦值;
(Ⅲ)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
科目:高中数学 来源:2012-2013学年甘肃省天水市高三第三次考试文科数学试卷(解析版) 题型:解答题
(本小题12分)如图所示,三棱柱A1B1C1—ABC的三视图中,正(主)视图和侧(左)视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点.
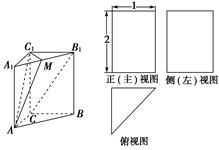
(1)求证:B1C∥平面AC1M;
(2)求证:平面AC1M⊥平面AA1B1B.
查看答案和解析>>
科目:高中数学 来源:2014届山西省高二10月月考理科数学试卷(解析版) 题型:解答题
(本小题12分)如图,  、
、 分别是正四棱柱
分别是正四棱柱 上、下底面的中
上、下底面的中
心, 是
是 的中点,
的中点, .
.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ当 取何值时,
取何值时, 在平面
在平面 内的射影恰好为
内的射影恰好为 的重心?
的重心?

查看答案和解析>>
科目:高中数学 来源:2014届安徽宿松县复兴中学高一第二学期第三次月考数学试卷(解析版) 题型:解答题
(本小题12分)
已知函数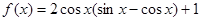 .
.
(1)求函数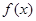 的最小正周期、最小值、最大值;
的最小正周期、最小值、最大值;
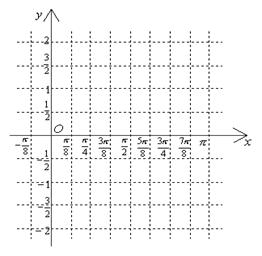
(2)画出函数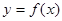 区间
区间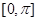 内的图象.
内的图象.
查看答案和解析>>
科目:高中数学 来源:2010年哈尔滨三中高一下学期第二模块数学卷 题型:解答题
(本小题12分)
正三棱柱 中,所有棱长均相等,
中,所有棱长均相等, 分别是棱
分别是棱 的中点,
的中点,
截面 将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体.
将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体.
 ①求几何体Ⅰ和几何体Ⅱ的表面积之比;
①求几何体Ⅰ和几何体Ⅱ的表面积之比;
②求几何体Ⅰ和几何体Ⅱ的体积之比.
查看答案和解析>>
科目:高中数学 来源:2010-2011年新疆农七七师高级中学高二下学期第一学段考试理科数学 题型:解答题
(本小题12分)
如图, <
< <
< <…<
<…< )是曲线C:
)是曲线C: 上的n个点,点
上的n个点,点 在x轴的正半轴上,且⊿
在x轴的正半轴上,且⊿ 是正三角形(
是正三角形( 是坐标原点)。
是坐标原点)。

(1)写出
(2)求出点 的横坐标
的横坐标 关于n的表达式并用数学归纳法证明
关于n的表达式并用数学归纳法证明
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com