
 .
.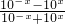 =-f(x),∴f(x)为奇函数
=-f(x),∴f(x)为奇函数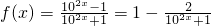
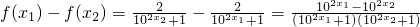
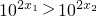 ,即f(x1)>f(x2)
,即f(x1)>f(x2) ,而102x>0,即
,而102x>0,即 ,∴-1<y<1.
,∴-1<y<1. 利用102x的范围求值域即可.
利用102x的范围求值域即可.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源:2012届安徽省泗县双语中学高三摸底考试理科数学 题型:解答题
附加题(本大题共两个小题,每个小题10分,满分 20分,省级示范性高中要
把该题成绩计入总分,普通高中学生选作)
已知 ,
,
(1)判断函数在区间(-∞,0)上的单调性,并用定义证明;
(2)画出该函数在定义域上的图像.(图像体现出函数性质即可)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三摸底考试理科数学 题型:解答题
附加题(本大题共两个小题,每个小题10分,满分 20分,省级示范性高中要
把该题成绩计入总分,普通高中学生选作)
已知 ,
,
(1)判断函数在区间(-∞,0)上的单调性,并用定义证明;
(2)画出该函数在定义域上的图像.(图像体现出函数性质即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com