
 x2+bx+c=0有一个根介于x1和x2之间.
x2+bx+c=0有一个根介于x1和x2之间.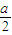 x2+bx+c,利用条件推出f(x1)f(x2)<0,即可说明方程
x2+bx+c,利用条件推出f(x1)f(x2)<0,即可说明方程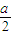 x2+bx+c=0有一个根介于x1和x2之间.
x2+bx+c=0有一个根介于x1和x2之间.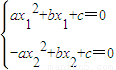
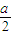 x2+bx+c,
x2+bx+c, x12+bx1+c=-
x12+bx1+c=-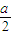 x12,
x12,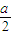 x22+bx2+c=
x22+bx2+c=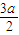 x22,
x22, a2x12x22
a2x12x22 x2+bx+c=0有一个根介于x1和x2之间.
x2+bx+c=0有一个根介于x1和x2之间.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
| a | 2 |
查看答案和解析>>
科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:044
x1与x2分别是实系数一元二次方程ax2+bx+c=0和-ax2+bx+c=0的一个根,且x1≠x2,x1≠0,x2≠0.求证:方程![]() x2+bx+c=0有且仅有一根介于x1与x2之间.
x2+bx+c=0有且仅有一根介于x1与x2之间.
查看答案和解析>>
科目:高中数学 来源:0128 期中题 题型:证明题
设x1,x2分别是实系数方程ax2+bx+c=0和-ax2+bx+c=0的一个根,且x1≠x2,x2≠0,
求证:方程 x2+bx+c=0有仅有一根介于x1和x2之间。
x2+bx+c=0有仅有一根介于x1和x2之间。
查看答案和解析>>
科目:高中数学 来源:2011年云南省高三数学一轮复习章节练习:函数的应用(解析版) 题型:解答题
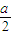 x2+bx+c=0有一个根介于x1和x2之间.
x2+bx+c=0有一个根介于x1和x2之间.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com