
| A. | (-$\frac{5}{4}$,1) | B. | ($\frac{3}{4}$,1) | C. | ($\frac{4}{5}$,1) | D. | (-1,$\frac{3}{4}$) |
分析 由题意和偶函数的性质求出f(x)的解析式,化简后可得f2(x),将f(x)=$\sqrt{x+a}$两边平方后,画出函数y=x+a与y=f2(x)的图象,并画出两条临界线,由特殊点和导数的几何意义分别求出a的值,将方程根的个数问题转化为函数图象交点个数的问题,由图象求出实数a的范围.
解答 解:设x<0,则-x>0,
∵当x≥0时,f(x)=|x-1|,∴f(-x)=|-x-1|=|x+1|,
∵f(x)是定义在R上的偶函数,∴f(x)=f(-x)=|x+1|,
则f(x)=$\left\{\begin{array}{l}{|x-1|,x≥0}\\{|x+1|,x<0}\end{array}\right.$,即${f}^{2}(x)=\left\{\begin{array}{l}{(x-1)^{2},x≥0}\\{(x+1)^{2},x<0}\end{array}\right.$,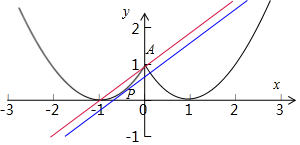
由f(x)=$\sqrt{x+a}$得,f2(x)=x+a,
画出函数y=x+a与y=f2(x)的图象,如图所示:
由图知,当直线y=x+a过点A时有三个交点,
且A(1,1),此时a=1,
当直线y=x+a相切与点P时有三个交点,
由图知,y=f2(x)=(x+1)2=x2+2x+1,
则y′=2x+2,令y′=2x+2=1得x=$-\frac{1}{2}$,则y=$\frac{1}{4}$,
此时切点P($-\frac{1}{2}$,$\frac{1}{4}$),代入y=x+a得a=$\frac{3}{4}$,
∵方程f(x)=$\sqrt{x+a}$有4个不相等的实根,
∴函数y=x+a与y=f2(x)的图象有四个不同的交点,
由图可得,实数a的取值范围是($\frac{3}{4}$,1),
故选B.
点评 本题考查函数奇偶性的性质,函数与方程的应用,利用数形结合是解决本题的关键,综合性较强,有一定的难度.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
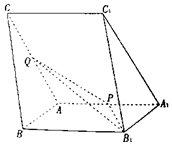 如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.
如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
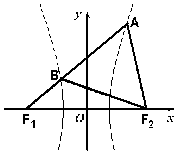 如图,F1、F2分别是双曲线的左、右焦点,过F1的直线与双曲线的左、右两支分别相交于B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为( )
如图,F1、F2分别是双曲线的左、右焦点,过F1的直线与双曲线的左、右两支分别相交于B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{7}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5+2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | $\sqrt{7}$ | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com