解:(1)令log
ax=t,x>0,则t∈R,x=a
t,
代入得f(t)=

(a
t-a
-t),
将t换成x,得到表达式f(x)=

(a
x-a
-x),x∈R.
∴f′(x)=
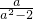
(a
x㏑a+a
-xlna)
=

×lna×(a
x+a
-x)>0
∴函数f(x)=

(a
x-a
-x),x∈R,是增函数.
(2)∵f(x)=

(a
x-a
-x),x∈R,
∴f(-x)=

(a
-x-a
x)=-f(x).
∴函数f(x)是奇函数.
∵定义在(-1,1)上的函数f(x),f(1-m)+f(1-m
2)<0,
∴f(1-m)<-f(1-m
2)=f(m
2-1),
∵f(x)是增函数,
∴
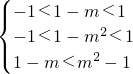
,解得0<m<1.
∴m的取值范围是(0,1).
(3)∵f(x)-4<0,在区间(-∞,2)上恒成立,
∴f(x)<4恒成立,∴f(x)
max<4.
∵f(x)是增函数,
令x=2,代入方程,得

<4.
整理得a
2-4a+1<0,
解得-

+2<a<

+2
又∵a>0且a≠1取交集,
∴a的范围是(-

+2,1)∪(1,

+2).
分析:(1)令log
ax=t,x>0,则t∈R,x=a
t,代入得f(t)=

(a
t-a
-t),由此能求出f(x)的解析式并判断其单调性.
(2)由f(x)是奇函数,且是增函数,定义在(-1,1)上的函数f(x),f(1-m)+f(1-m
2)<0,知
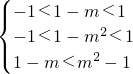
,由此能求出m的取值范围.
(3)由f(x)-4<0,在区间(-∞,2)上恒成立,知f(x)
max<4.由f(x)是增函数,令x=2,代入方程,得

<4.由此能求出a的范围.
点评:本题考查函数的解析式的求法,考查函数的单调性的判断,考查满足条件的实数的取值范围的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

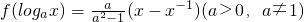 ,
, (at-a-t),
(at-a-t), (ax-a-x),x∈R.
(ax-a-x),x∈R.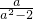 (ax㏑a+a-xlna)
(ax㏑a+a-xlna) ×lna×(ax+a-x)>0
×lna×(ax+a-x)>0 (ax-a-x),x∈R,是增函数.
(ax-a-x),x∈R,是增函数. (ax-a-x),x∈R,
(ax-a-x),x∈R, (a-x-ax)=-f(x).
(a-x-ax)=-f(x).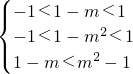 ,解得0<m<1.
,解得0<m<1. <4.
<4. +2<a<
+2<a< +2
+2 +2,1)∪(1,
+2,1)∪(1, +2).
+2). (at-a-t),由此能求出f(x)的解析式并判断其单调性.
(at-a-t),由此能求出f(x)的解析式并判断其单调性.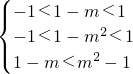 ,由此能求出m的取值范围.
,由此能求出m的取值范围. <4.由此能求出a的范围.
<4.由此能求出a的范围.
