
 ,AP=
,AP= ,PC=
,PC= .
.
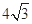 .
. ∥BC,且
∥BC,且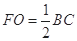 ,
,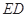 ∥BC,且
∥BC,且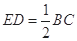 ,
, ∥ED,且
∥ED,且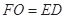
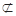 平面PDC
平面PDC 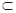 平面ABCD,
平面ABCD,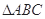 与
与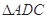 面积相等,
面积相等,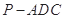 与三棱锥
与三棱锥 体积相等,
体积相等,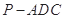 体积的二倍.
体积的二倍.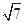 ,
,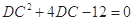 , 解得DC=2 ------------------- 10分
, 解得DC=2 ------------------- 10分 三棱锥
三棱锥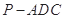 的体积
的体积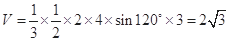
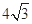 -------------------- 12分
-------------------- 12分

科目:高中数学 来源:不详 题型:解答题
 ;
; 的体积;
的体积; 

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的三视图如图所示,其中俯视图和侧视图都是腰长为
的三视图如图所示,其中俯视图和侧视图都是腰长为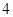 的等腰直角三角形,正视图为直角梯形.
的等腰直角三角形,正视图为直角梯形. 的体积为
的体积为 ,求实数
,求实数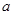 的值;
的值; ,求异面直线
,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;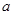 ,使得二面角
,使得二面角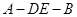 的平面角是
的平面角是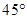 ,若存在,请求出
,若存在,请求出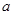 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.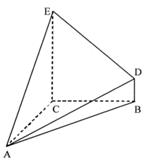

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,OC=
,OC= ,则三棱锥O-ABC外接球的表面积为( )
,则三棱锥O-ABC外接球的表面积为( )| A.4p | B.12p | C.16p | D.40p |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com