练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    动点P到点F(1，0)的距离与它到直线l：x＝－1的距离相等，记点P的轨迹为曲线C1．圆C2的圆心T是曲线C1上的动点，圆C2与y轴交于M，N两点，且|MN|＝4．

    (Ⅰ)求曲线C1的方程；

    (Ⅱ)设点A(a，0)(a＞2)，若点A到点T的最短距离为a－1，试判断直线l与圆C2的位置关系，并说明理由．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：河北省邯郸市临漳一中2012届高三春季开学摸底考试数学文科试题 题型：022

    下列四个命题：

    ①若m∈(0，1]，则函数的最小值为；

    ②已知平面α，β，直线l，m，若l⊥α，mβ，α⊥β，则l∥m；

    ③△ABC中和的夹角等于180°－A；

    ④若动点P到点F(1，0)的距离比到直线l：x＝－2的距离小1，则动点P的轨迹方程为y2＝4x．

    其中正确命题的序号为________．

    查看答案和解析>>

    科目：高中数学 来源：山东省潍坊市2012届高三下学期考前仿真模拟(五)数学文科试题 题型：022

    下列四个命题：

    ①若m∈(0，1]，则函数的最小值为；

    ②已知平面α，β，直线l，m，若l⊥α，mβ，α⊥β，则l∥m；

    ③△ABC中，和的夹角等于180°－A；

    ④若动点P到点F(1，0)的距离比到直线l：x＝－2的距离小1，则动点P的轨迹方程为．

    其中正确命题的序号为________．

    查看答案和解析>>

    科目：高中数学 来源：福建省漳州一中2013届高三5月月考数学文试题 题型：044

    平面内动点P到点F(1，0)的距离等于它到直线x＝－1的距离，记点P的轨迹为曲线Γ．

    (Ⅰ)求曲线Γ的方程；

    (Ⅱ)若点A，B，C是Γ上的不同三点，且满足＋＋＝0．证明：△ABC不可能为直角三角形．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年湖北省武汉市高三11月调考文科数学试卷（解析版） 题型：解答题

    已知平面内一动点P到点F(1，0)的距离与点P到y轴的距离的差等于1．

    （Ⅰ）求动点P的轨迹C的方程；

    （Ⅱ）过点F作两条斜率存在且互相垂直的直线l1，l2，设l1与轨迹C相交于点A，B，l2与轨迹C相交于点D，E，求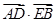的最小值．

     

    查看答案和解析>>

    同步练习册答案